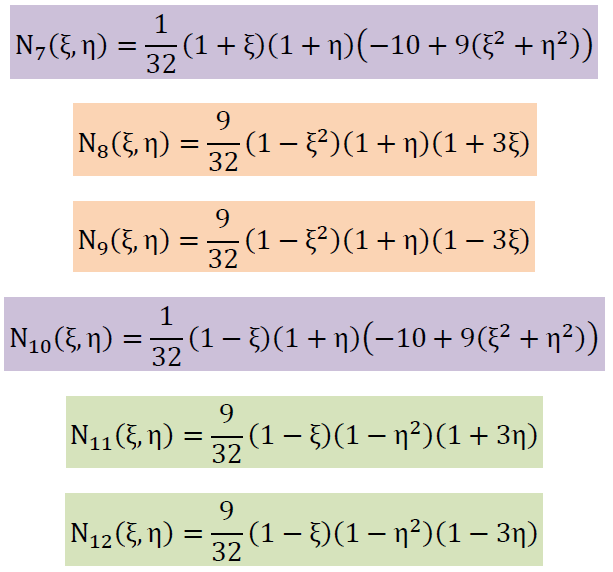
上の式が形状関数のルールに適合しているかどうかチェックは表計算ソフトのエクセルかまたは簡単なプログラムを書いて行うことができます。その中には、 N₁+N₂+N₃+N₄+N₅+N₆+N₇+N₈+N₉+N₁₀+N₁₁+N₁₂=1 が確認できるようになっていると便利です。

■コメント■
これで、　2次元のIso-parametric 要素の説明は、終わりますが、理解できましたでしょうか。理解すると、自分で様々要素を作ることが出来ます。

最後に私から、2次元Iso-parametric要素の特徴についてコメントしておきます。

要素当たりの節点数を増やすと(要素を高次にすると)、未知数の近似解の精度は、確かに向上します。しかし、プログラムが、安定した解析精度を供給してくれるかどうかは、疑問です。解の安定性は、要素の数学的対称性に大きく関係しているからです。よって、Iso-parametric要素の中では、4-Nodedが一番安定していることになります。勿論、3-Nodedの三角形要素が数学的に最も安定していますが、解析精度が低いことと、要素数が多くなると言う理由から実用的ではありません。

8-Nodedと9-Nodedを時間依存の解析に使う場合は、時間項の処理に特別な処置が必要になります。私の場合、時間依存の流体解析が専門ですから、私は、もっぱら特別な処置が不要な4-Noded Iso-parametric 要素を使っています。

次は、3次元のIso-parametric要素を紹介します。