1次元で紹介したGauss積分では、Summationが一重でした。2次元では、二重積分ですから、Summationも下に示す様に二重になります。

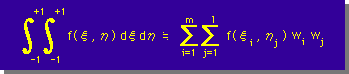
■数値積分の計算方法■
Sampling Points が2つのGauss-Legendre法を用いて、二重Summationを計算してみましょう。必要な材料は、Sampling Pointsの座標値とWeighting factorです。1次元で紹介したGauss積分を参照して下さい。
では、二重Summationを展開してみましょう。次の様になります。

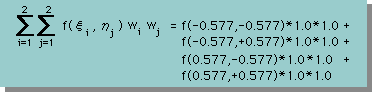
Sampling Pointsの位置は、下図に示してあります。貴方は、上式の右辺の4つの項目が､それぞれ、図のどの位置に対応しているか確認して下さい。

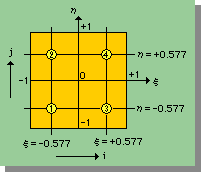
これで、4-Noded Iso-parametric要素については、全て学習したことになります。理解できましたか？。勉強することが沢山あったので、ちょっと頭が混乱しちゃいましたか？。確かに、三角形要素に比べると、プログラムがかなり複雑なります。貴方もプログラムを書いてみて下さい。勉強の手助けになりますよ。とにかく、最低Iso-parametric要素をマスターしないと、有限要素法の世界へは、入り込めません。是非、元気を出してなんべんでもトライして、自分の物にして下さいね。まー、とりあえず、ビールですね。つまみは、黒豆の枝豆ですかね。