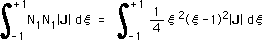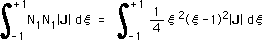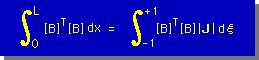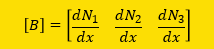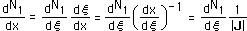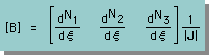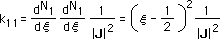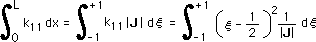One Dimensional Finite Element Method
Parabolic Element-5
またJacobian Matrix の行列値に形状関数を代入すると次の様になる。

|J| = 0.5(2ξ-1)x1 + (-2ξ)x2 + 0.5(2ξ+1)x3

参考までにN1N1の計算をしてみましょう。 結果は下の様になり手計算が面倒であればGauss-Legendre積分法で求めることが出来ます。 後で紹介するプログラムもGauss-Legendre積分法で積分を行っています。

上が正しいかどうかは貴方がチェックしてください。

■[B]T[B]の積分■
次に[B]T[B]の積分のやりかたを紹介します。 まず積分は下式に示すように無次元座標系に変換できます。

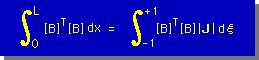式中の[B]は下に示す通り1x3 マトリックスになります。

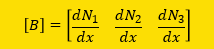もっと解り易くするためにdN1/dxの計算を下に示します。N1は直接xで微分出来ないので Chainrule を使って目的の微分を行っています。2次元や3次元で明白になってくるのですが、dx/dξ=[J]で dξ/dxは[J]の逆行列になります。そして|[J]|または|J|はその逆行列の行列値です。しかし1次元では [J]は1×1のマトリックスですので、|J|は(dx/dξ)-1で計算されることになります。

したがって、[B]マトリックスを無次元座標系で書くと下図のようになります。

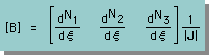[B]T[B] を [kij] とおくとk11とその積分は次の様になります。

BACK NEXT
Menu View Helm wrm Lin Element Rmrk Vari Para Non-L Wire
Internet College of Finite Element Method