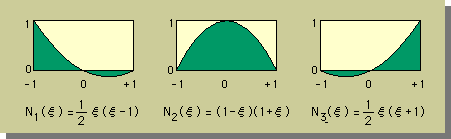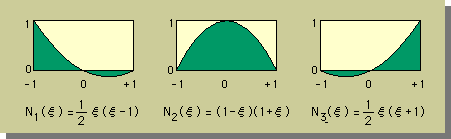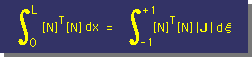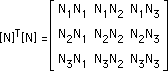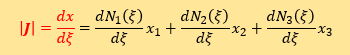One Dimensional Finite Element Method
Parabolic Element-4
すると式中のu(ξ)は形状関数を用いると次の様にかけます。
全ての形状関数が無次元座標ξの関数であることに注目して下さい。
| u(ξ) = N1(ξ)u1 + N2(ξ)u2 + N3(ξ)u3 |
では実座標のxと無次元座標のξとの関係は どうなっているのでしょうか。
答えは簡単です。
xもu(x)同様に、独立関数として扱えば良いのです。
実際ξからみればx(ξ)も独立関数です。
結果は下の様になります。
| x = N1(ξ)x1 + N2(ξ)x2 + N3(ξ)x3 |
さて条件を満足している形状関数は どの様な形をしているのでしょうか。
下図がそうです。
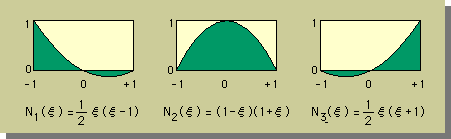貴方は上の式が形状関数の条件に満足していることをチェックして下さい。
■形状関数の作り方■
N1(ξ)の作り方を例に取り上げます。
N1(ξ)はξ=0とξ=+1でゼロですね。
それら2点でゼロになる関数は、ξと(ξ-1)ですよね。ですからN1(ξ)=aξ(ξ-1)になります。aは定数です。
次にN1(-1)=1になるように定数aを決めます。
■[N]T[N]の積分■
材料が揃ったところで手始めに[N]T[N]の積分を行ってみましょう。
実際の積分については1次要素のところで沢山勉強しましたので ここでは手法のみを紹介します。
実座標系での[N]T[N]の積分は次の様に無次元座標系へ変換されます。
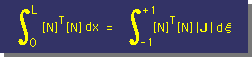ここに、要素長さL = x3 - x1
そして
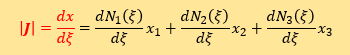となります。
BACK
NEXT
Menu
View
Helm
wrm
Lin
Element
Rmrk
Vari
Para
Non-L
Wire
Internet College of Finite Element Method
