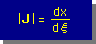
例えば [N]T[N]や[B]T[B]の積分です。 上の形状関数を使うと、これらの積分が非常に面倒になります。 ここでは 2次以上の高次要素のことも考慮して座標変換とGauss-Legendre積分法を用いた有限要素法を紹介します。 また プログラムもすっきりして見易くなります。形状関数を作るのも楽になります。
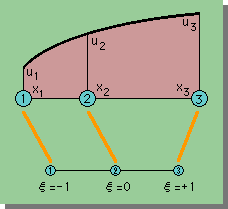
まず下の図をご覧下さい。 実座標のx1、x2、x3がそれぞれ無次元座標のξ=-1、ξ=0、ξ=+1 に対応しています。
座標変換については 数値積分のところでも紹介しましたので そちらも参考にして下さい。 以前は線形座標変換でしたが ここでは 座標変換の式も2次式になります。
まず実座標上の関数u(x)をx1からx3まで積分することを考えます。 そして実座標の独立変数xを無次元座標の独立変数ξに変換します。 そのためにチェーンルールで構成されているJacobian Matrix [J] の行列値 |J| を使います。 1次元の場合はマトリックスでなくスカラーになります。 つまり dx=(dx/dξ)dξですから |J| は次の様になります。