■積分式■
先ほど導いた熱拡散方程式は、時間依存です。つまり、時間的に温度が変化する状態を再現または予測してくれます。しかし、有限要素法を最初に学ぶには、ちょっと難しすぎますので、時間項をドロップします。時間項をドロップした熱拡散方程式をLaplace Equation と言い、下の左の式の様になります。式の( ) の中は、q_iであることに注意しておいて下さいね。(正確には、k₁₂ = k₂₁ = 0 で、k₁₁ = k₂₂ = 1 の状態のときを、Laplace Equation と言います。 )
Laplace EquationのTに近似解を代入すると、残差(R(T))が発生します。ここでは、残差を下の右の式の様に定義します。1次元のときと、なんら変りはありませんね。

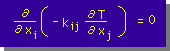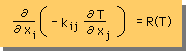残差が定義されると、後の手続きは簡単ですよね。まずは、下に積分式を示します。

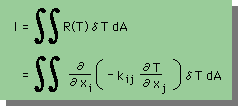
領域積分項に部分積分を施すと、下式が得られます。2次元の部分積分法については、CALCULUS in FEM を参考にして下さいね。

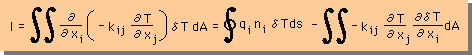
q_n = q_in_i で表わし、上式をちょっと整理すると、次が得られます。

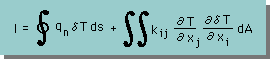
さらに、温度 T(x,y) を要素の近似式で表現した場合、積分式は、次の様になります。いきなり matrix 表示の積分式が出てきて、びっくりしたと思います。後程、詳細な説明を準備していますので安心して下さい。

ここに、[M]は1次元の時の[N]と同じと思って間違いありません。また、この時点において、まだ要素の形および節点数は設定されていません。[E]は、熱伝導マトリックスです。詳細は後で紹介します。
上の式に対し、∂I/∂{δT}^T = を計算すると、要素の連立方程式が得られます。これらの計算についても、後程、詳細に紹介します。
上の式は、一見、難しそうに思えますが、Looks は1次元とほぼ同じであることに気付くでしょう。ただ、Laplace Equation には、生成項がないだけです。後程、2次元Helmholtz Equation のFEM プログラムも紹介します。