Anisotropic 熱伝導係数による Heat Flow をもっと奇麗に書き表わす方法が有ります。それは、Tensor表示法です。下式を見て下さい。Index の i が Free Index で、j がDummy Index です。Dummy Index が1つの項に2つ現われていますから、Index Notation のルールに従い、和を計算します。
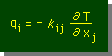
熱伝導係数 kij の様にindex が2つある要素を、 Second Order Tensor と言います。
Anisotropicが取り扱えるソフトでも、Insotropicの材料の熱解析を行いたいことがあります。どうすれば、このAnisotropic 熱伝導係数をInsotropic にするにすることが出来るか、考えてみましょう。 次の様にすればよいことになります。
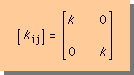
■2次元熱拡散方程式(つづき)■
さて、熱伝導係数の説明が一段落したところで、話しを、Heat Equation に戻します。思い出して頂くために、下にHeat Balance Equation を表示します。
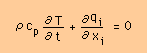 |
この上の式に、先ほどのAnisotropic 熱伝導係数を用いた Heat Flow の式を代入します。結果は、下式の様になります。熱伝導係数のkijは、ρcpで割られ、kijになっています。
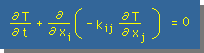
この式には、2つのIndices i と j があります。両方とも Dummy Index ですから和をとります。つまり、二重Sumになります。
上の式は、かなり一般的な熱拡散方程式になっています。様々なコンティニュームメディアに適応できます。
Index 表示でなく、通常のxとyで式を書き替えると、次に示す様な長い式になります。
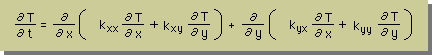
先ほども言いましたが、kxy = kyx とすると、次の様になります。
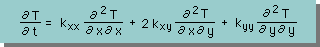
これで、一応、Heat Equation の式の導きは終わりました。次は、有限要素式を導き出します。有限要素式については、1次元のHelmholtz Equation のところでさんざん勉強しましたので、次のWRMでは、詳しい説明は省きます。
 |
 |
|---|
| BACK | NEXT-WRM_2dim |
|---|
| Menu | Heat Eq. | Cdtvty | WRM2 | Tri | Stiff | Bound | Ex | Rmk |