■1次元熱拡散方程式(復習)■
次元が1つ多くなると、問題は急に難しくなります。プログラミングにも時間がかかるようになりますので、貴方も少しエネルギーを蓄積してからこの2次元に挑んで下さい。
2次元熱拡散方程式に挑戦する前に、1次元熱拡散方程式を導いてみましょう。下の図をご覧下さい。
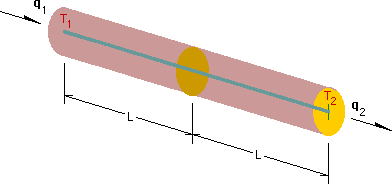
金属の丸棒に熱流束(q)が左から右へ伝導している状態を示しています。熱流束は、Heat Fluxのことで、領域の境界面での熱の流れを意味します。そして、領域内では、Heat Flowと言います。両方とも熱の流れであることには、違いありません。
熱流束(q)の単位はcal/time/areaです。丸棒の表面は、絶縁されているものとします。したがって、丸棒に流入した熱流束はロスすることなく(実際はロスが有る)内部を伝わり、丸棒内に温度変化を発生させます。
ここで、熱の収支を考えてみましょう。丸棒の始点と終点(境界)に、違う値の熱流束が存在すれば、丸棒内の温度も変化するはずです。つまり、”t+Δt時の丸棒内の熱量上昇=Δt間での熱流束の流入”と言えます。また、”t+Δt時の丸棒内の熱量上昇-Δt間での熱流束の流入=0”とも言えます。更に、以下の様にも書けます。
| t+Δt時の丸棒内の熱量上昇+Δt間での熱流束の流出=0 |
|---|
これをHeat Balance Equation と言います。ここで、熱量(h)=ρcpTとします。ρ=丸棒の密度(Density)、cp=比熱(Specific heat at constant pressure(cal/g/℃)、T=温度です。
これを数式で書くと次の様になります。
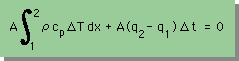
ΔT=温度の上昇、A=丸棒の断面積、Δt=微小時間である。そして、丸棒に流れている熱は、Q=qAです。
ところで、境界積分の q2-q1は、積分のルールを使うと、どの様に書けるか知っていますか。次の様になりますね。
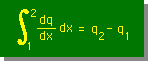
これは、1次元のDaivergence理論と言って良いでしょう。
| BACK-1次元 | NEXT |
|---|
| Menu | Heat Eq. | Cdtvty | WRM2 | Tri | Stiff | Bound | Ex | Rmk |