■境界積分の項■
次に境界積分項の計算方法について説明します。有限要素法において、下に示す境界積分の項は、わりと大ざっぱな計算をします。

何故かと言うと、境界積分の計算結果は、節点に集約されるため、計算に多少の誤差が有っても、つじつまさえ合っていればOKだからです。貴方も、そのうち、上述の意味が解ってくるでしょう。
まず、下の図を見て下さい。ちょっとごちゃごちゃしていますが、よーく見ると何が描かれているかが、解ってきます。
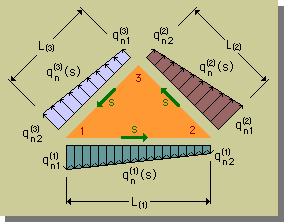
図中の三角形は、要素です。三角形の境界線には、Heat Fluxがあります。図に示すように、Heat Fluxは、境界線に対し外向きがプラスです(境界でのHeat Flowは、Heat Fluxと呼ばれます)。その他、ここで使っている関数および変数を、下表にまとめておきました。
| 境界線 | 節点番号 -->節点番号 | 境界線の 長さ | Heat Flux | Heat Flux at s=0 | Heat Flux at s=L |
|---|---|---|---|---|---|
| 1 | 1-->2 | L(1) | qn(1)(s) | qn1(1) | qn2(1) |
| 2 | 2-->3 | L(2) | qn(2)(s) | qn1(2) | qn2(2) |
| 3 | 3-->1 | L(3) | qn(3)(s) | qn1(3) | qn2(3) |
マトリックス表示法による、各境界線上のHeat Fluxは、1次元のHelmholtz Equation の時に用いた1次要素の形状関数と全く同じです。ただ、領域積分と境界積分とを区別するために、ここでは、形状関数マトリックスの[N]の代わりに[M]を使います。下に3つの境界線上のHeat Fluxの式を示します。
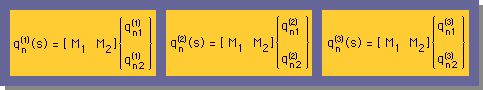
ここに、形状関数マトリックス[M]の内訳は、下図の様になっています。独立変数(s)を除いては、1次元1次要素と同じです。
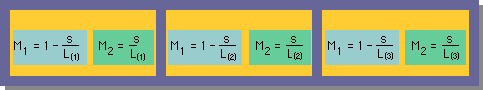
| BACK to Stiffness Matrix | NEXT |
|---|
| Menu | Heat Eq. | Cdtvty | WRM2 | Tri | Stiff | Bound | Ex | Rmk |