■等方性熱伝導係数■
熱伝導係数には、様々な型が有ります。
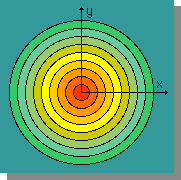
まず、等方性(Isotropic)について説明します。鉄板の一点を、半田ゴテで加熱します。すると、一点の温度は上昇し、そして、その周辺の温度も上昇してきます。温度分布の広がり方は、熱伝導係数の値によって違いますが、右図の様に等円を描きます。つまり、どの方向にも温度の伝わるスピードが同じであることを意味しています。

図の様な温度分布になるためには、x軸上のq_xとy軸上のq_yでは、q_x=q_yになっているはずです。また、図を観察するとx軸上の∂T/∂xとy軸上の∂T/∂yでは、∂T/∂x = ∂T/∂y になります。言い換えると、∂T/∂r=f(r),∂T/∂θ= 0 になっています。つまり、熱伝導係数は、k = k_x = k_yです。したがって、Heat Flow は、以前紹介したように下式で求めることが出来ます。

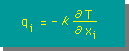
殆どの技術問題は、材料が熱的に等方性あると仮定して計算します。

■Orthotropic 熱伝導係数■
材料は、等方性だけでは有りません。方向によって、温度分布が変化することがあります。下図では、x方向とy方向では、熱の伝わり方の違う鉄板を用意して、等方性のときと同じ実験を実施した温度分布を表わしています。

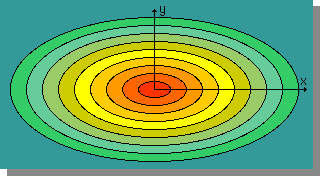
結果は、q_x≠q_yです。
もう少し、深く温度分布を観察してみましょう。x軸に沿って温度の変化を見てみると、∂T/∂x ≠0 であり、等方性と同じ様に∂T/∂y=0です。また、y軸方向についても同様な結果が得られます。つまり、Orthotropic 材料の場合、Heat Flow は、下式の様に書けます。

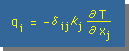
Index i は、free index で、 j は dummy index です。