■2次元熱拡散方程式(つづき)■
話しが、かなり横道へそれました。2次元のHeat Balance Equatuon を思い出して頂くために、もう1度、下に式を表示します。

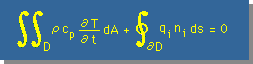
上式の線積分の項にDivergenceの定理を施すと、下図の左の様になります。また、領域の大きさは任意であると言うことから、下図の右の微分方程式が得られる。

式の中のq_iは、以前紹介しましたが、もう一度、ここでも表示しておきます。

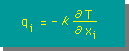
この Heat Flow の式は、Fourier 則とも言われています。この Heat Flow の式を、上の微分方程式に代入すると、下図の2次元 Heat Equation が得られます。 (Heat Equation は、Indexと通常の表示方法で書かれています。もちろん、両方との同じです。)

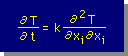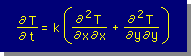ここに、k=k/(ρc_p) である。

上の式は、2次元熱拡散方程式とも言われます。また、この式は、等方性の熱伝導係数(k)であることに注意して下さい。

問題

疑問および質問