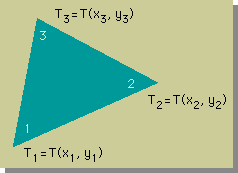■三角形要素■
2次元で最もシンプルでフレキシブルな要素が、三角形です。また、三角形要素は、2次元で数学的に対称な近似式を備えた、たった1つの要素でもあります。ちょっと話しが難しくなりましたが、簡単に言うと、2次元で一番安定した要素だと言うことです。しかし、現在では三角形要素を使う人が少なくなりました。理由は、解析精度が良くないのと、三角形要素で要素分割すると入力のデータ量が増えるからです。私も、もう使いません。最近は、次に紹介するParametric要素を使っています。

しかし、三角形要素は、2次元有限要素法の勉強を始めるにのに、最適な要素ですので、話しを進めさせてもらいます。下に三角形要素を示します。

各三角形の頂点に節点が有り、節点番号として、1、2、3 が割り当ててあります。各節点の位置は、xとy座標で決められています。また、各節点では、未知数である温度(T)が与えられています。さらに、三角形要素で節点数が3ですから、節点間の温度変化は、線形(Linear)になります。

1次元の要素と同じように、2次元の要素を構成する上でも、幾つかのルールがあります。まず、要素上の節点番号を参照するときは、反時計方向に数えます。なんとなく理解に苦しむ説明ですが、下の図を参考にして、理解を深めて下さい。

この参照方法を反時計方向にする1つの理由として、三角形要素の面積計算に右手の法則が使えるからです。下の図を見て下さい。三角形要素の2辺を、ベクトルAとBで書き表わしています。

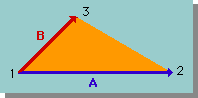	A = (x2-x1)i + (y2-y1)j
	B = (x3-x1)i + (y3-y1)j