すると、三角形要素の面積は、その2つのベクトルの外積で求めることが出来ます。外積のルールとして、AxB = - BxAがあることを理解しておいて下さい。よって、三角形要素の面積は次の様になります。
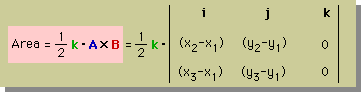
もっと、詳細に書くと、下の様になります。
| Area(三角形の面積) = (1/2)*((x2-x1)(y3-y1) - (x3-x1)(y2-y1)) |
次に、三角形要素の近似式を考えみましょう。まず、x-y 座標で、2点を通過する直線の式は、y=ax+b ですね。つまり、2点だと、直線を決定する未知数(a, b)が2つになります。
三角形要素の場合は、どうでしょう。x-y-T 座標で、3点を通過する平たい面の式は、次の様になります。
| T(x, y) = a + bx + cy |
式は出来ましたが、じゃ、”どうやって a, b, c を決める”かです。
誰でも考える方法としては、各節点の座標値と温度を上式にほうりこんで、3X3マトリックスの連立方程式を解くと、a, b, c は得られます。しかし、これは賢い方法ではありません。せっかく、形状関数の作り方を1次元で勉強したので、 a, b, c の決定に、形状関数のルールから攻めてみましょう。
形状関数がどんなものかは、まだ、わかっていませんが、もし、形状関数が有れば、三角形要素内の温度分布は、次の様になります。
| T(x, y) = N1(x,y)T1+ N2(x,y)T2+ N3(x,y)T3 |
さらに、温度の代わりに座標(独立変数)を上式に代入すると、次の様にxとyを表わすことが出来ます。
| x = N1(x,y)x1+ N2(x,y)x2+ N3(x,y)x3 |
| y = N1(x,y)y1+ N2(x,y)y2+ N3(x,y)y3 |
それに、形状関数の究め付けは、3つの形状関数の和をとると、常に1になることです。つまり、下の式です。
| 1 = N1(x,y)+ N2(x,y)+ N3(x,y) |
| BACK | NEXT |
|---|
| Menu | Heat Eq. | Cdtvty | WRM2 | Tri | Stiff | Bound | Ex | Rmk |