形状関数が3つですから、3つの線形の式があれば、形状関数は定まることになります。つまり、次の連立方程式を解くと、形状関数は決定できます。
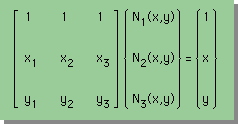
下が、その形状関数です。
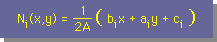
ここに、A は三角形要素の面積です。bi、ai、ciは、以下の様になっています。
| i | bi | ai | ci |
|---|---|---|---|
| 1 | y2-y3 | x3-x2 | x2y3-x3y2 |
| 2 | y3-y1 | x1-x3 | x3y1-x1y3 |
| 3 | y1-y2 | x2-x1 | x1y2-x2y1 |
形状関数が求まれば、三角形要素内の温度分布と重み関数は、以下に示す様なマトリックス形式で書くことができます。

ここに、
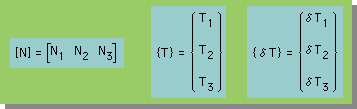
です。
 |
 |
|---|
| BACK | NEXT |
|---|
| Menu | Heat Eq. | Cdtvty | WRM2 | Tri | Stiff | Bound | Ex | Rmk |