■領域積分のマトリックス表示■
ここでは、2次元 Weighted Residual Method で導いた領域積分項の離散化について説明します。下がその領域積分です。
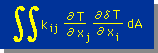
1次元のHelmholtz equation のところでもも言いましたが、この積分から得られるマトリックスのことを、通称"Stiffness Matrix"と言います。正確には、Navierの式の2階微分項からなる領域積分のことをStiffness Matrixといいますが。
まず、Heat Flow(qi) をρcpで割った値を、q'iとします。 そして、q'iをIndexで表わすと、下の右の様になります。
| q'i = qi/ρcp | 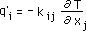 |
すると、領域積分は、次の様に書けます。貴方も確認して下さい。
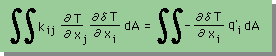
上の式をx-y 座標変数で書くと、下の様になります。
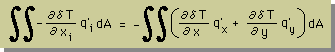
さらに、上の式をマトリックス表示法で書くと、次の様になります。貴方も確認して下さい。
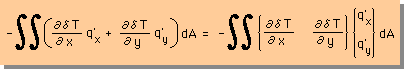
領域積分項のマトリックス表示法については、1次元のところで詳しく説明してあります。
| BACK to Triangular Element | NEXT |
|---|
| Menu | Heat Eq. | Cdtvty | WRM2 | Tri | Stiff | Bound | Ex | Rmk |