さらに、マトリックス表示法のトランスボーズを用いると、次の様に書けます。
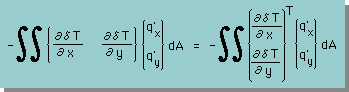
ここまでは、問題なく理解できましたか。少しでも分からなくなったら、すぐ前のステップに戻って下さい。
次へ進みます。ここで、もう一度、{q'}をマトリックス表示法で書いておきます。下がそうです。
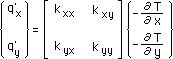
■領域積分の離散化■
三角形要素の形状関数を使うと、T(x,y) = [N]{T}でしたから、温度(T(x,y))の微分は次の様に書けます。これは、1次元のところで勉強しましたので、もし、理解できなければ、1次元のFinal Remarkへ戻って復習して下さい。
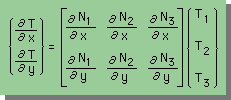
ここに、1次元同様、形状関数の微分を、下に示す様に[B]マトリックスで表わします。
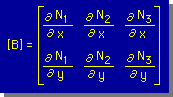
| BACK | NEXT |
|---|
| Menu | Heat Eq. | Cdtvty | WRM2 | Tri | Stiff | Bound | Ex | Rmk |