その1次元Divergence理論を使い、そしてΔt を限りなく小さくすると、Heat Balance Equation は、次の様になります。
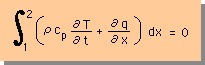
微分を示すdが偏微分記号になったのは、Tとqが、xとtの関数であるからです。
上式の積分範囲について、ちょっと話しをしましょう。上の積分範囲である1から2は、私が勝手に決めた範囲です。貴方が式を導いていたなら違った積分範囲になっていたでしょう。つまり、積分範囲は任意に決められているのです。しかし、積分される内容は、変わりません。よって、上式を下の左の様に書くことが出来ます。式の中のDは、領域(Domain)のDを意味します。 また、積分範囲が任意で、式の右辺が=0であると言うことは、積分される内部の式が=0であると言うことになります。つまり、下の右の式です。
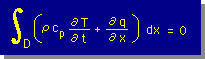 |
または | 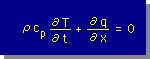 |
|---|
ところで、Heat Flow(q)は、いったい何者でしょう。Heat Flow は、温度の関数として書けないものでしょうか。実験によると、熱は、温度の高い点から低い点にめがけて流れます。つまり、次の経験式が実験から得られています。
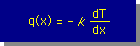
ここに、kは、丸棒の熱伝導係数(Thermal conductivity of a substance)です。この経験式を、Fourier's law ともいいます。
さて、qが何者かが分かったところで、上式をHeat Balance Equation に代入してみましょう。次の様になるはずです。
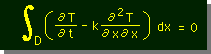 |
または | 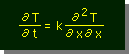 |
|---|
ここで、k=k/(ρcp) である。右の式は、Heat Equation としてよく見かける形です。kの単位は、長さの二乗割る時間[L2/T]であることに注意してください。
| BACK | NEXT |
|---|
| Menu | Heat Eq. | Cdtvty | WRM2 | Tri | Stiff | Bound | Ex | Rmk |