■2次元熱拡散方程式■
やっと2次元の話しが出来るようになりました。まずは、2次元の領域を見て下さい。下がそうです。
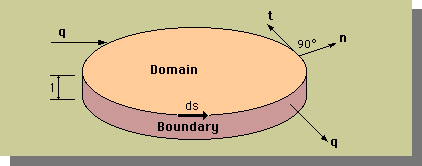
Domainと書いてある面とその裏面は、断熱してあると仮定します。
Heat Flux (q)は、領域(Domain)の境界(boundary)から出たり入ったりしています。2次元になるとqは、x方向とy方向のコンポーネントを持っています。そのためにqはベクトルになります。
tとnは、それぞれ境界に対し接線(Tangential)と法線(Normal)方向の単位ベクトルです。接線ベクトルは、dsと同じ方向を、そして法線ベクトルは境界から外向きを正(+)とします。領域の厚さは、1です。
下の図は、境界を含む領域の一部を示しています。熱が境界から逃げて行くところを描いています。赤色の部分は、微小面積です。面積は、Δs*1です。
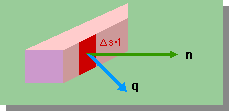
すると、その微小面積から出て行く熱流束(Q)は、次の様になります。
| Q = q・nds * 1 |
ここに、nは微小面積上の法線(Normal)ベクトルです。内積q・nにより、境界面から放出される熱が計算されます。もし、qが境界面に平行なベクトルであると、q・n=0 になります。つまり、熱は外へ出ていないことになります。貴方も、上の式が正しいかどうか確かめて下さいね。
ここで、ちょっとdsとベクトルt、n、qについてまとめておきます。
まず、境界上の微小長さdsは、次の様に定義されています。この定義は、あくまでもx-y 直交座標を用いたときに限ります。
| ds2 = dx2 + dy2 |
そして、接線ベクトルと法線ベクトルは、次の様な性質が有ります。
| 接線ベクトル(t) | 法線ベクトル(n) | 特 徴 |
|---|---|---|
| t=(dxi+dyj)/ds | n=(dyi-dxj)/ds | t・n = 0 n×t・k = +1 |
| t・t = 1 | n・n = 1 |
ここで注意しておきますが、ベクトルの外積(Cross Product) は、n×tの順序が正です。t×nは、-kを生成します。また、この2つのVectorsの関係からNormal vector は、n=t×kで求めることができます。
| BACK | NEXT |
|---|
| Menu | Heat Eq. | Cdtvty | WRM2 | Tri | Stiff | Bound | Ex | Rmk |