次にheat flow の式ですが、1次元の式を拡張すれば、わりと簡単に導くことが出来ます。ただし、2次元のheat flow の式は、ベクトルであると言うことを頭に入れておいて下さい。つまり、次の様に書けます。
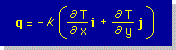
ここで注意しなくてはならないことは、x方向とy方向の熱伝導係数です。この場合は、両方とも同じであるから等方性熱伝導係数と言います。殆どの材料が等方性(Isotropic)として取り扱ってもOKですが、板状の素材を張り合わせた材料は、等方性ではありません。
話しを熱流束(q)に戻します。先程は、境界での微小面積からの熱流束の求め方を学びました。Q=q・ndsでした。では、全境界ではどうでしょう。この全熱流束を求めるために、線積分(Line Integral)を使います。次の様に書きます。

ここで、また、ちょっとベクトルの内積(Dot Product)について、触れておきます。下図を見て、内積の特徴を理解しておいて下さい。
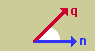 | ベクトル間の角度が90度以内の場合 | 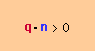 |
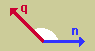 | ベクトル間の角度が90度以上の場合 | 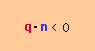 |
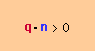 | qが領域から流出している。 | |
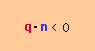 | qが領域へ流入している。 | |
| BACK | NEXT |
|---|
| Menu | Heat Eq. | Cdtvty | WRM2 | Tri | Stiff | Bound | Ex | Rmk |