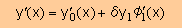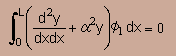One Dimensional Finite Element Method
Calculus of Variations-5

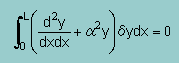■変分法とWRMは同じ■
上の式(前のページ)を よーく見るとWRM(重み付け残差法)で紹介した積分式とまったく同じですね。

WRM のときはHelmholtz equation に重み関数をかけそれを領域積分しゼロと置きました。 そして2階微分項に部分積分を施しましたね。

ここでは近似解が厳密解に近づくための条件を変分法で導きました。 つまりδI=0 です。 両者が同じということは ここで紹介した 状態関数 はHelmholtz equation の 状態関数 であるということを証明してくれていることになりますね。

またWRM(重み付け残差法) では下の左の式に示す様に”微分方程式に重み関数(δy(ｘ))乗じて領域積分し それを強制的にゼロにする。 そして 2階微分項に部分積分を施す”でしたよね。 もう分かったと思いますが実は下の左に示すWRMの積分式は変分法から導き出された結果(右の式)だったのです。

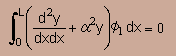または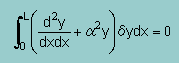

そして もっと重要な事は変分(δy(ｘ))が重み関数だったのです。 なんと マーですよね。 よーく考えると変分(δy(ｘ))の形状には　なんの制限も有りませんでしたよね。 と言うことは重み関数の形状にも なんの制限もないことになる訳ですよ。

■Euler-Lagrange Equation■
このセッションの始めのころに変分法の先駆者はJean Bernoulli(1667-1748) と言いました。 歴史上確かにそうなんですが　ここで紹介している変分法を学問に仕上げる切っ掛けをつくった人物は　Joseph L. Lagrange (1736-1813) だったのです。 ここからは　Lagrange がどんな活躍をしたかを紹介します。 ちょっと話が難しくなりますので読みたくない人は 次の2次要素へ進んで下さい。

先ほど下に示す条件式を紹介しましたね。 下の式は 変分方向にTaylor展開すると出てくる項です。

上の式を展開すると次の様になります。 理解しずらいと思いますが よーく見ると ただ 状態関数 を　δy1 で微分しているだけです。 貴方もやってみてくださいね。

ところで近似解(y(x))は下式の様に定義しましたね。

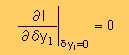
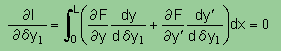
または、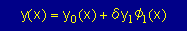

ですから近似解をxで微分すると次の様になりますね。

BACK NEXT
Menu View Helm wrm Lin Element Rmrk Vari Para Non-L Wire
Internet College of Finite Element Method