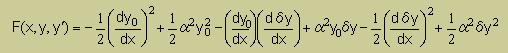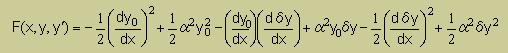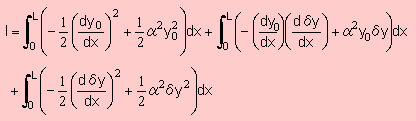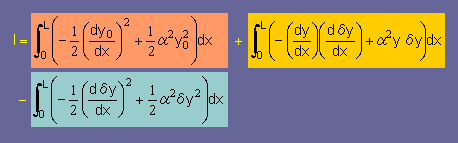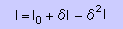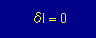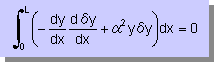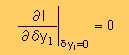One Dimensional Finite Element Method
Calculus of Variations-4
■δI=0の意味■
δy1 が変化したとき、 積分式の値(I) の状況を調べる最も簡単な方法として先ほど紹介した近似解(y(x)=y0(x)+δy(x))を 状態関数 に代入することです。
すると状態関数は次の様になります。
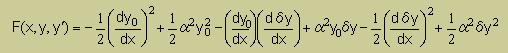 そして積分式(I) は次の様に書けますね。
そして積分式(I) は次の様に書けますね。
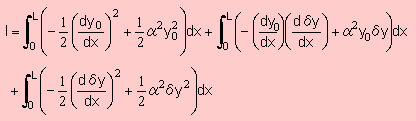 ここで上式の右辺の第2項の y0 を y0=y(x)-δy(x) で置き換えます。
すると上式の右辺の第2項のy0が y になり他の項は そのままになります。多少、符号は変わっていますがね。
結果的に上式は次の様になります。
ここで上式の右辺の第2項の y0 を y0=y(x)-δy(x) で置き換えます。
すると上式の右辺の第2項のy0が y になり他の項は そのままになります。多少、符号は変わっていますがね。
結果的に上式は次の様になります。
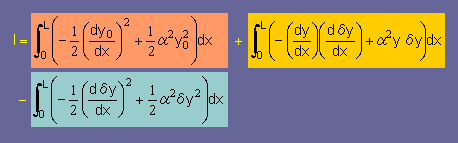 これを下式の様に書くことにします。
前にも言いましたが y0(x) を積分式に代入すると極値(最大または最小)のI0 を生産しますね。
これを下式の様に書くことにします。
前にも言いましたが y0(x) を積分式に代入すると極値(最大または最小)のI0 を生産しますね。
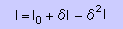 ここで何を追求していたかと言うと近似解y(x)を厳密解y0に近づける条件を探していました。
つまり上式の I が I0 に近づく条件ですね。
ここでδy は とても小さい値だと仮定していますので δy2 を含む δ2I はゼロと置きます。
すると I = I0 にするには下の左の条件が満足しなければなりませんね。
つまり下の右の積分式になりますね。
ここで何を追求していたかと言うと近似解y(x)を厳密解y0に近づける条件を探していました。
つまり上式の I が I0 に近づく条件ですね。
ここでδy は とても小さい値だと仮定していますので δy2 を含む δ2I はゼロと置きます。
すると I = I0 にするには下の左の条件が満足しなければなりませんね。
つまり下の右の積分式になりますね。
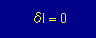 |
=====>> |
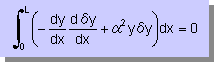 |
ここで、δI の積分式には (1/2) が無いということに注目して下さい。
また下式に示す様に δy(x)=δy1φ1(x) ですから積分(I)をδy1で微分しても δI=0 の積分式と同じ様な式になりますね。
変数δy1でδI=0 の両辺を割った状態になっていますね。
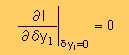 |
=====>> |
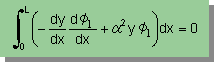 |
さて肝心のy(x)ですが上の積分式を満足する y(x) を作り出せばよいことになります。
これって どこかで見ましたよね。
そーです。
WRMのところで見ました。
計算方法については重み付け残差法で既に紹介しましたよね。
BACK
NEXT
Menu
View
Helm
wrm
Lin
Element
Rmrk
Vari
Para
Non-L
Wire
Internet College of Finite Element Method