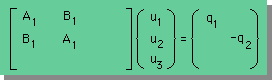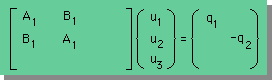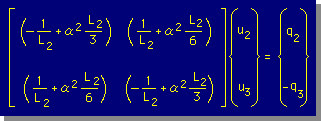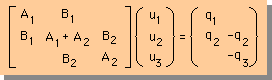One Dimensional Finite Element Method
Integral By Element-4
■最初のAssembly■
この2x2の連立方程式をグローバルマトリックスの3x3の連立方程式に足し込んでみましょう。
足し込むといっても3x3の連立方程式まだ空ですから書き込むだけに過ぎないですが。
下図の様になりますね。
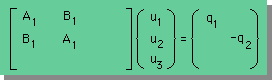 ここにAiとBiは1次要素で紹介した式と同じです。
ここにAiとBiは1次要素で紹介した式と同じです。
■要素2での積分■
次に要素2の上で積分式の計算を実行します。
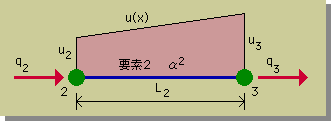
まず要素2上での未知数と変数を下図に示しておきます。
要素1と違う点は節点番号と変数の添え字だけです。
 そして要素1同様に積分を行います。
要素1と違う点が積分の上限・下限値だけですから計算の必要はないですね。
以下に積分結果を2x2の連立方程式としてまとめてみました。
そして要素1同様に積分を行います。
要素1と違う点が積分の上限・下限値だけですから計算の必要はないですね。
以下に積分結果を2x2の連立方程式としてまとめてみました。
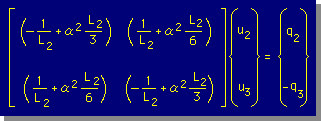 要素1との相違点は、変数および未知数の添え字だけです。
要素1との相違点は、変数および未知数の添え字だけです。
■2回目のAssembly■
要素2の2x2の連立方程式が出来上がったところで再び先程の3x3の連立方程式に足し込んでみましょう。
要素2の節点番号が2と3であるから要素2の連立方程式は3x3の連立方程式の2行と3行の2列と3列に足し込まれることになります。
下図の様になるはずです。
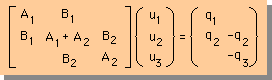 出来上がった3x3の連立方程式のマトリックスをGlobal Matrix といいます。
ところで、上の3x3の連立方程式の右辺の上から2番目のq2-q2はInter-Element Continuity の条件からゼロになることに注意して下さいね。
すると上の連立方程式は1次要素で導いた連立方程式とまったく同じ結果になります。
つまり[K]{u}={RHS}である。
出来上がった3x3の連立方程式のマトリックスをGlobal Matrix といいます。
ところで、上の3x3の連立方程式の右辺の上から2番目のq2-q2はInter-Element Continuity の条件からゼロになることに注意して下さいね。
すると上の連立方程式は1次要素で導いた連立方程式とまったく同じ結果になります。
つまり[K]{u}={RHS}である。
また境界条件の組み込み方法については1次要素のDirichlet境界条件の組み込みを参照して下さい。
連立方程式の解法についてはnumericalのsimultaneousをご覧下さい。
BACK
NEXT
Menu
View
Helm
wrm
Lin
Element
Rmrk
Vari
Para
Non-L
Wire
Internet College of Finite Element Method