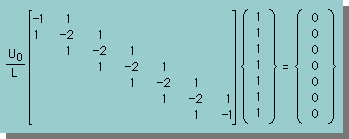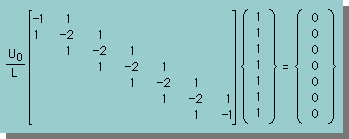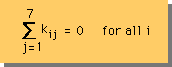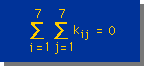One Dimensional Finite Element Method
Final Remark-9
次に、q1=q7=0 を考慮します。
つまり抵抗線に電流が流れていない状態です。
すると抵抗線のどの位置の電圧を測定しても同じ値を示すはずです。
この時の電圧を U0 とすると {u}=U0{1}となり連立方程式は次の様になります。
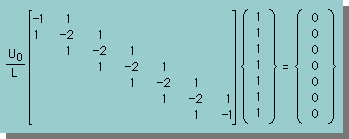便宜上、上の連立方程式を [kij]{1}={0} or [K]{1}={0} で表すことにします。
つまり上の連立方程式が伝えようとしていることは下式と同じことになります。
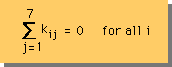上の式は、全ての値の i に言えることですので、下式も正しいことになります。
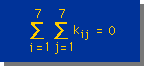この特徴を使うと[K] マトリックスの対角要素を計算することが出来ます。
下式がそうです。
注意：Summation では j=i は含みません。
さらに、[K] は、対称マトリックスです。
これは連立方程式を解く上で大きな得点であることは既に
Matrix
で述べました。
2階微分項が教えてくれることで、もう1つ重要な事があります。
それは境界条件の1つはDirechlet型でなくてはならないということです。
つまり q1とq7に値を与えても電圧は決定出来ないですからね。
このことから言えることは Direchlet型境界条件を組み込む前の マトリックス[K]の行列値 (Determinant) はゼロであることになる。
つまり
である。
BACK
NEXT
Menu
View
Helm
wrm
Lin
Element
Rmrk
Vari
Para
Non-L
Wire
Internet College of Finite Element Method