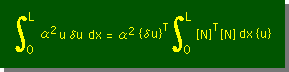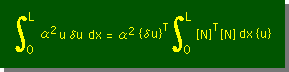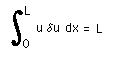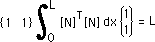One Dimensional Finite Element Method
Final Remark-10
■生成項(Source Term)の特徴■
新しい重み関数を用いた積分式の生成項は下式の様でした。
生成項とは Helmholtz Equation のα2の項のことです。
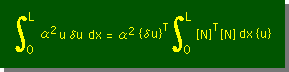生成項の特徴を引き出すために α2=u(x)=δu(x)=1 とします。
ベクトルも{u}={δu}={1}となります。
するとこの条件で生成項を積分すると結果は要素の長さになります。
同様にマトリックス表示の生成項も同じ結果を出さなければならない。
つまり下式です。
 |
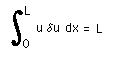同様に、 |
 |
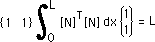便宜上、上の[N]T[N]の積分を次の様に定義します。
するとマトリックス[GEOM]の中味を全部足し算すると要素の長さ L になります。
この結果は有限要素法による解析システムを作り上げる上で最低限えられなくてならない事です。
理由は以前、形状関数の説明のところで形状関数の1つの条件として N1(x)+N2(x)=1 がありましたね。
つまりΣNi(x)=1 です。
これは1次要素の場合ですが、その他の要素や2次元3次元の要素でもこの条件は適用されます。
つまりこの条件が守れていないと[N]T[N]の積分結果が 要素の長さ(L) にならないことになります。
2次元3次元では、それぞれ要素の面積と体積になります。
BACK
NEXT
Menu
View
Helm
wrm
Lin
Element
Rmrk
Vari
Para
Non-L
Wire
Internet College of Finite Element Method