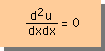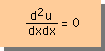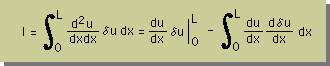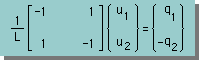One Dimensional Finite Element Method
Final Remark-8
■2階微分項の特徴■
一通り有限要素法の基礎の勉強が終了したところで有限要素法の副産物について説明します。
まず有限要素法のテクニックを使って2階微分項の物理的意味を紹介します。
説明のために下の微分方程式を考慮します。
つまり Helmholtz Equation のα2の項が無い式です。
この方程式は抵抗線内の電圧分布u(x)を表わすことが出来ます。
未知数の微分 du/dx は電流を表します。
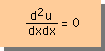 すると積分式 I は部分積分を使って次の様に書き替えられます。
すると積分式 I は部分積分を使って次の様に書き替えられます。
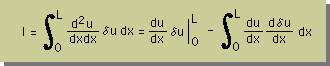 1次要素を用い積分を実行すると要素のマトリックス型有限要素式が得られます。
下がそうです。
1次要素を用い積分を実行すると要素のマトリックス型有限要素式が得られます。
下がそうです。
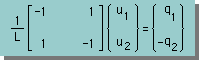 まず計算の対象となる領域として適当な長さの抵抗線を考慮します。
そしてその抵抗線を 6等分に要素分割します。
1つの要素の長さは L です。
次に各々の要素のマトリックス型有限要素式を Assemble すると下の連立方程式が得られます。
まず計算の対象となる領域として適当な長さの抵抗線を考慮します。
そしてその抵抗線を 6等分に要素分割します。
1つの要素の長さは L です。
次に各々の要素のマトリックス型有限要素式を Assemble すると下の連立方程式が得られます。
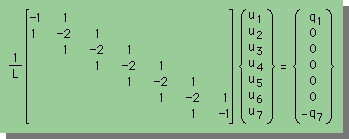 仮に抵抗線内に電流が存在し q1=q7 とします。
すると電圧の値は分からないが電圧の分布は線形になるはずです。
つまり電圧は一定でないことを意味しています。
抵抗線の表面からの熱損失は無いものとします。
仮に抵抗線内に電流が存在し q1=q7 とします。
すると電圧の値は分からないが電圧の分布は線形になるはずです。
つまり電圧は一定でないことを意味しています。
抵抗線の表面からの熱損失は無いものとします。
BACK
NEXT
Menu
View
Helm
wrm
Lin
Element
Rmrk
Vari
Para
Non-L
Wire
Internet College of Finite Element Method