Electromagnetics and Ham Radio
Offcenterfeddp 03

上の式には複素数のj等のクロスの項目がないため、 Ax, Ay, Az の式は単独で存在し、また、波源は点の集合体で再現できるものとして仮定すると、下の3次元無限領域スカラー変数の Helmholtz波動方程式がとければよいことになります。

\begin{eqnarray} \frac{\partial^2G(\mathbf{x},\mathbf{\xi})}{\partial x_i\partial x_i}+k^2G\left(\mathbf{x},\xi\right)+\delta(\mathbf{x},\mathbf{\xi})=0 \end{eqnarray}

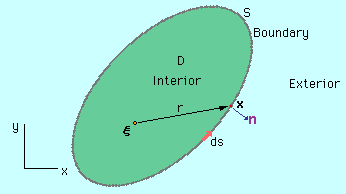
ここにxはδ(x,ξ) =波源(Source point)の点、ξが観測点(Observation point)になります。 Source point とObservation point の関係を2次元の図で表すと下図のようになります。下図は有限領域の例ですが、無限領域ではInteriorとExteriorが入れ替わります。波源(Source point)の点はInteriorまたはBoundaryへ移動します。

インダクタンスとキャパシタンスの場合、伝送線路の断面での電界と磁界の直流による2次元計算でしたので上式に有るk2の項がありません。
そして3次元の上式の解は以下になります。

\begin{eqnarray} G\left(\mathbf{x},\mathbf{\xi}\right)=\frac{1}{4\pi}\frac{exp\left(-jkr\right)}{r} \end{eqnarray}

式中のrはSource point(x)とObservation point(ξ)間の距離になります。 これをGreen関数とも呼びます。 Green関数を使った数値解析を境界要素法(BEM)と言い、本サイトやインダクタンスとキャパシタンスの計算のところでも紹介してありますので、そちらも参考にして下さい。 Green関数は同じ名前の方程式(例えばラプラス方程式)でも次元によって解が違います。
話は脱線しますが、Green関数のGeorge Green(1793年7月14日 - 1841年3月31日）は、19世紀の物理学者および数学者でした。 本サイトで紹介しているBEMはGreen関数無しでは存在しません。
Greenの定理も有名です。 応用として 2次元の複数のセグメントで閉じた面積の計算があります。 本サイトでも紹介しています。 彼は40歳でどちらかと言うと行きたくなかったケンブリッジ大学に入学し卒業後47歳でこの世を去っています。 彼の業績は素晴らしく、図書館名に彼の名前が使われています。私もGreen関数を使った数値的解法を好んで使っています。 話を本題に戻します。

Preceding Page Next Page
Menu Inductance Capacitance Exp Z0 Coaxial Balun Dielectric Off-Center-fed DP Helmholtz FEM BEM
Internet College of Finite Element Method
JR2XSO