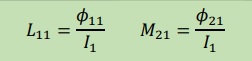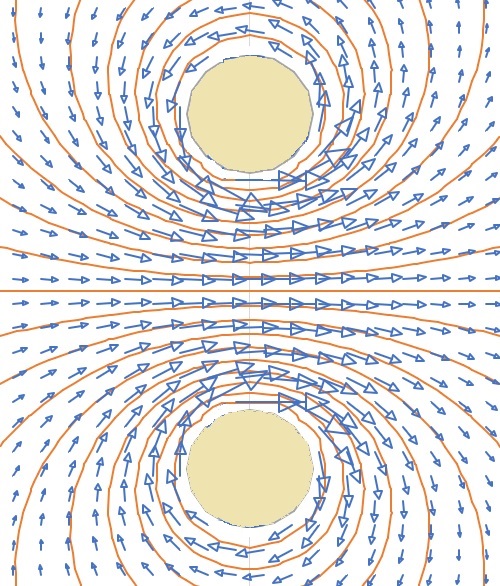
下図の2つの円は、導線の断面です。左の導線には+1[A]そして右の導線には-1[A]の直流電流が 流れた時に発生する磁束密度のベクトルと磁気ベクトルポテンシャル の等高線を表しています。 ペア導線のインダクタンスは、この磁気ベクトルポテンシャルを使って計算します。 ここでは、磁気ベクトルポテンシャルの方程式の導出とインダクタンスの計算方法を 紹介します。

■自己インダクタンスと相互インダクタンスの定義■
インダクタンスは、下式に示す様に磁束(Φ)はインダクタンス(L)と電流(I)との積というの関係式で定義されています。

上式を実際の計算に落とし込むためには、下図に示す磁束を計算する方法を見つけなければなりません。 図の赤色の導線の輪C₁に直流電流I₁が流れています。 すると右ねじの法則に従い輪の面に対してノーマル(垂直)方向に抜けるように磁束Φ発生します。 単位面積当たりの磁束を磁束密度Bで表します。

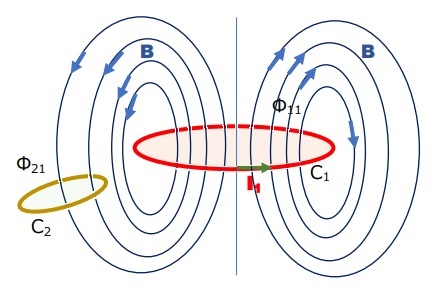C₁に鎖交する磁束をΦ₁₁、C₂に鎖交する磁束をΦ₂₁とすると、 自己インダクタンス(L)と相互インダクタンス(M)は、次式で計算できます。

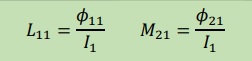ここでは、今後この計算結果を特性インピーダンスに使うため、 自己インダクタンス(L)のみの計算方法を紹介します。