 Electromagnetics and Ham Radio
Electromagnetics and Ham Radio
Offcenterfeddp

ダイポールアンテナ一本のみで出来るだけ多くの周波数にQRV出来ないかと思いネット検索したところWINDOMまたは
Off-Center-Fed Antennaに辿り着き、このサイトを書くことになったのです。
そのためには50Ω対200Ωのバランの理屈を知る必要がありました。
バランは伝送線路であるためインダクタンス(L)とキャパシタンス(C )を計算する勉強が必要でした。
有限要素法(FEM)と境界要素法(BEM)を使って定常(Steady)のLとC計算ができるようになったというのが、これまでの経緯です。
ここからはアンテナの入力インピーダンスを計算する手法を勉強しなければなりませんが、これまでにLとCの理解に必要な事柄が役に立ちそうです。
というのも、LとCのベースはLaplace方程式でしたが、
アンテナでは時間微分項がAexp(iωt)に置き換えられたHelmholtz方程式になります。
つまり、Helmholtz方程式はLaplace方程式にAexp(iωt)が足された式に成っています。
数値計算としては無限境界を簡単に扱えるBEMが良さそうです。
Laplace方程式をFEMで計算するのは計算領域の境界で反射がないので問題ありませんが、Helmholtz方程式の場合計算領域の境界で反射が発生します。
これを反射なしにするために面倒なことを施さなければなりません。
ですので、ここではBEMで話を進めます。
■Off-Center-Fed Dipole Antennaについて■
通常λ/2ダイポールアンテナは、中央で給電します。
その給電位置をずらしていった場合、インピーダンス(Z=R+X)の放射抵抗(R)は各周波数でどのように変化するかです。
計算方法については後で詳しく触れますが、λ/2ダイポールアンテナの給電位置を変えた時の放射抵抗(R)の計算結果は下図の様になります。
縦軸は入力インピーダンス(Z)のRです。
横軸は、アンテナ中央で0そして右端のλ/4の位置で1に無次元化した距離を示します。計算にはMMANAを用いました。
アンテナの全長は21.11214m+ 21.11214mの42.22428mです。この長さは3.55MHzの電流分布がアンテナの両端でゼロになる長さです。
短縮率は考慮していません。
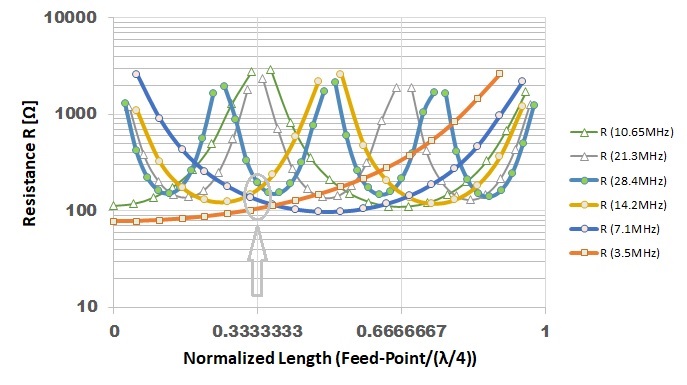
横軸の0.333333の位置は、アンテナの右端(または左端)から全長の1/3のところです。
給電した周波数は、3.55MHz, 7.1MHz, 14.2MHz, 28.4MHzです。
この点の放射抵抗Rを見ると100Ω~200Ωの間にあります。インピーダンスマッチングには送信機のアンテナチューナーを使う必要がありますが、1本のアンテナで4つの周波数にQRVできます。
21.3MHzと10.65MHzもおまけで計算しておきました。
これらの周波数では、この1/3の点で電流がゼロになるため放射抵抗が無限大になっています。
アンテナを希望の周波数にマッチングさせるには、リアクタンス(X)をゼロにする必要があります。
つまり、共振点のX=0Ωです。これについては後でMMANAを使って短縮率を計算してみます。
Preceding Page: Last Page of dielectric
Next Page
Menu
Inductance
Capacitance
Exp
Z0
Coaxial
Balun
Dielectric
Off-Center-fed DP
Helmholtz
FEM
BEM
Internet College of Finite Element Method
JR2XSO
