 Electromagnetics and Ham Radio
Electromagnetics and Ham Radio
Coaxial

■同軸ケーブルに関する数値解析■
ペア導線ではポアソン方程式かまたはラプラス方程式を境界要素法で解き
インダクタンス(L)とキャパシタンス(C)を計算しました。そしてLとCから特性インピーダンスを
導きました。
同軸ケーブルでも同様にインダクタンス(L)とキャパシタンス(C)を計算し特性インピーダンスを概算します。
しかし、ネットや書物を見ると同軸ケーブルではラプラス方程式でインダクタンスとキャパシタンスを
計算しています。つまり、
Ampere's Law
と
Gauss's Law
を用いているため、同軸ケーブルの芯線内の磁気ベクトルポテンシャル
と電位の分布を必要とするポアソン方程式は計算に使っていません。
ここでも、まず1次元軸対称のラプラス方程式で厳密解を導き特性インピーダンスを計算してみます。その後、
軸対称の有限要素法で芯線に電流か電荷が有る状態の解析が出来るプログラムを開発する方法を紹介します。
2次元ラプラス方程式の境界要素法でも特性インピーダンスを計算してみます。この場合は、同軸ケーブルの
断面を境界要素で分割するのですが、ここでは2次要素を使ってみます。ペア導線の場合は1次要素でした。
ついでに同軸ケーブルの外側の導体が正方形や長方形だった場合の特性インピーダンスの計算を試みてみます。
計算と実際が一致しているかどうかは、実験をする必要があります。ここでは計算ののみとします。
■軸対称の微分方程式■
同軸ケーブルは芯線を軸に軸対称になっています。
よって1次元軸対称ラプラス方程式で計算を進めることができます。
1次元とは言っても角度方向(θ)に対称ということは、結果的に2次元ということです。
方程式は数学の文献や工学の文献に記載されていますので式の導出についてはそちらを参考にして下さい。
電位を使って式を書くとポアソン方程式は以下のようになっています。
|
\begin{eqnarray}
-\frac{d}{dr}\left(r\frac{dV}{dr}\right)=\frac{q(r)}{\varepsilon}
\end{eqnarray}
|
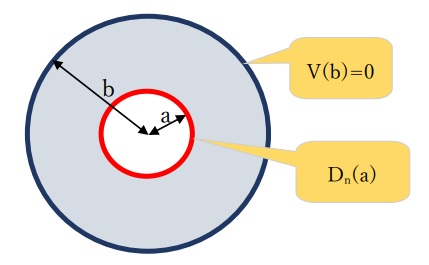
ここにVは電位、電荷q(r)は下図に示す同軸ケーブルの芯線に与えられる分布電荷です。
この電荷は誘電率εで割った値です。式の展開およびプログラムによる計算の実行は、ε=1で行っています。
上式は分布電荷があるため一般解は有りません。
芯線(内部導体)の半径をa、芯線の中心から編組線(外部導体)までの距離をbとします。
芯線(
Inner conductor
)と編組線(
Outer conductor
)の間は、絶縁体が充填されています。
絶縁体はポリエチレンか発泡ポリエチレンでできていて比誘電率は約2.3です。
 ペア導線のインダクタンスとキャパシタンスの数値解析で紹介したように、
計算に分布電荷qを含める方法(領域積分型境界要素法)とGauss's Lawを活用した境界積分型境界要素法を紹介しました。
ここでもまずGauss's Lawを活用しインダクタンスとキャパシタンスを算出する方法を紹介します。
ペア導線のインダクタンスとキャパシタンスの数値解析で紹介したように、
計算に分布電荷qを含める方法(領域積分型境界要素法)とGauss's Lawを活用した境界積分型境界要素法を紹介しました。
ここでもまずGauss's Lawを活用しインダクタンスとキャパシタンスを算出する方法を紹介します。
Preceding Page: Z0
Next Page
Menu
Inductance
Capacitance
Z0
Exp
Balun
Coaxial
Off center fed DP
Helmholtz
FEM
BEM
Internet College of Finite Element Method
