Coaxial2

Electromagnetics and Ham Radio
Coaxial2

■同軸ケーブルの微分方程式の厳密解■
分布電荷qを集中電荷とし、Gauss's Lawによる電束密度を絶縁体の芯線に接触している側に与えるので、式はラプラス方程式になり以下のように記述できます。

\begin{eqnarray} -\frac{d}{dr}\left(r\frac{dV}{dr}\right)=0 \end{eqnarray}

このように式が簡略化されると、以下の一般解が存在します。下式の対数関数のベースはeですので注意してください。

\begin{eqnarray} V(r)=C_0+C_1{log}_e\left(\frac{r}{r_0}\right) \end{eqnarray}

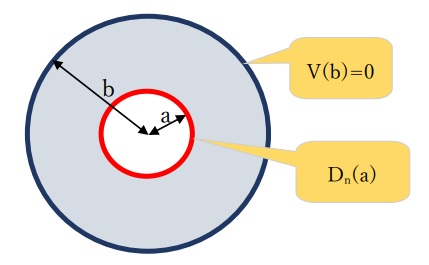
上の解には、２つの未知数がありますので、境界条件も2つ必要になります。１つが下図に示す絶縁体の外側の編組線(藍色の円)で電位が基準値のゼロになります。つまり、V(b)=0です。

もう１つが芯線の表面(赤色の円)で、Gauss's Lawから以下になります。

\begin{eqnarray} D_n(r)=\frac{Q}{2\pi a} \end{eqnarray}

D_n(r)=-ε(dV/dr)ですから、D_n(a)=- εC₁/aになりますので、この結果を上の一般解に代入すると、未知数の１つのC₁は以下になります。

\begin{eqnarray} C_1=\frac{Q}{2\pi\varepsilon} \end{eqnarray}