 Electromagnetics and Ham Radio
Electromagnetics and Ham Radio
Dielectric
 Page 01
■FEMによる誘電体を含むキャパシタンスの解析■
Page 01
■FEMによる誘電体を含むキャパシタンスの解析■
Balunで誘電体を含むキャパシタンスの解析の概略を説明しました。ここでは実際にFEM(有限要素法)を使って解いてみます。
これまではBEM(境界要素法)を使って問題を解いてきました。BEMは無限領域の取り扱いが簡単だったからです。
しかし、BEMは複数の誘電体が存在する場合は、ちょっと面倒な処理をする必要があります。
しかし、FEMは要素毎に誘電率を割り当てられますので計算は簡単です。しかし、無限領域の処理が面倒になります。
ここでは、計算領域を出来るだけ大きくとり、BEMの計算結果と比較し無限領域に近い値を出しているかチェックすることにしました。
上でも言いましたが、円が有る場合、FEMの要素分割は時間を要します。ここでは、いつも通りFORTRANで要素分割のプログラムを作成しました。
まず、下図を見てください。これはデモ用に少ない要素で領域を分割しています。
実際の計算では半径方向に分割数を多くし無限領域を再現しています。計算領域は、対称面の上半分です。
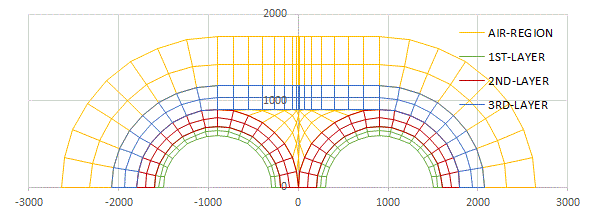 図にあるように極座標を使って要素分割をやっています。軸の単位は、μmです。
要素は全てBilinear Elementで分割してあります。
上の図は、半径方向に8分割で、角度方向に90度(π/2)を8分割しています。
分割で一番手の掛る部分は、2つの導線間の三角の空間です。
この三角の部分も全てBilinear Elementで分割してあります。
図にあるように極座標を使って要素分割をやっています。軸の単位は、μmです。
要素は全てBilinear Elementで分割してあります。
上の図は、半径方向に8分割で、角度方向に90度(π/2)を8分割しています。
分割で一番手の掛る部分は、2つの導線間の三角の空間です。
この三角の部分も全てBilinear Elementで分割してあります。
要素分割は、上図の色分けで分かるように4つの層に分けられています。
導線の表目にはエナメル塗布(1ST-LAYER)を考慮し半径方向に2要素で分割してあります。
その上に熱収縮チューブ(2ND-LAYER)を想定した2要素があります。
更に、2つの導線を密着させるための熱収縮チューブ(3RD-LAYER)の2要素も用意してあります。
その他は、空気の層(AIR-REGION)です。
無限領域を再現するには、上図の空気の層を厚くしなければなりません。
Preceding Subject: Balun
Next Page
Menu
Inductance
Capacitance
Exp
Z0
Coaxial
Balun
Dielectric
Off center fed DP
Helmholtz
FEM
BEM
Internet College of Finite Element Method
JR2XSO
