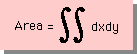
■Divergence の定理の副産物■
Divergence の定理の実用的な応用として、面積の計算があります。 Heat flow をq_x=xとq_y=y とすると(q_x=2xとq_y=0 or q_x=0とq_y=2y でもOK) 、前ページに表示されているDivergence の定理の領域積分は、divq=2ですから、2∬dA になります。 つまり、2倍の領域の面積(Area)です。また、面積を積分で表すと、下式になりますよね。

ですから、Greenの定理から次の式が出来上がります。

上の式を利用すると、任意の境界を持つ領域の面積を計算できます。 例えば、左下の図の様に境界が、直線のセグメントで書かれていると、上の式は、右下の式の様に離散化できます。 この離散化について詳しく知りたい方は、次をクリックして下さい。すると、手書きのノートPage one(52KB), Page two(56KB), Page three(40KB) が画面に表示されます。 表示された画像は、マウスのボタン操作で保存できます。

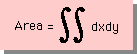
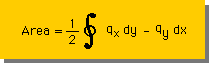
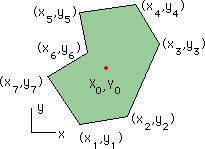
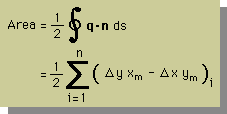
図形の重心(図心)の位置は、断面1次モーメントを計算することにより、求めることができますよね。つまり、重心の位置(X₀, Y₀)は、次の様に定義されています。

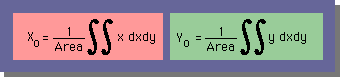
これらの計算をGreenの定理またはDivergenceの定理の式で行う場合、q_xとq_yを次の様に設定するとX₀, Y₀が求められます。 X₀の計算では、q_x=(1/2)x²、q_y=0 とします。そして、Y₀の計算では、q_y=(1/2)y²、q_x=0 とします。計算式の離散化については、次のページのJavaScriptを見て理解するか、連絡下さい。