■First Order■
有限要素法が出力する計算精度をチェックするには、どうしても厳密解が必要になりますよね。そこでは、一例として、常微分方程式(O. D. E.) の厳密解の出し方を紹介します。まずは、下の左の1階常微分方程式を取り上げます。厳密解は、u(0) を初期条件とすると、下の右の様になります。

どーってことは、ないですね。
話はちょっと難しくなりますが、時間項を含む微分方程式では、まず、重み付け残差法を用いスペース方向(x,y,zのこと)を離散化します。すると、連立1階常微分方程式が出来上がります。ですから、1階常微分方程式を効率的かつ精度よく解ける方法が見付かれば、問題は解決することになりますね。1階常微分方程式の数値解法については、時間項の処理のところで詳しく説明します。

ここでは、時間微分に関係のない例題を1つ紹介しておきます。それは、下図に示す様に、回転しないドラムにベルトがかけてある状態の例題です。 ”なーんだ、つまんない例題だなー”とお思いでしょうが、以外や以外や、実際によく見かけます。貴方もそこら辺を探してみて下さい。

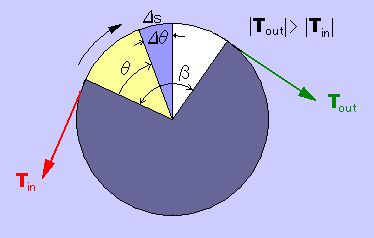
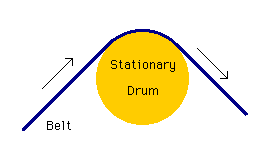ベルトは、左から右へドラムの上を滑りながら等速で進行しています。するとベルトとドラムの間では、摩擦が発生しますね。よって、下図に示す様に、ベルトの張力は、|T_out|>|T_in|　になりますね。 つまり、ドラムの右側のベルトの張力が高くなりますよね。