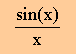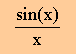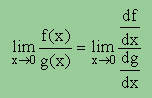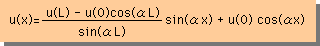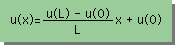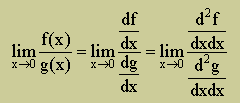■関数の極限■
有限要素法では、L'hospital's ruleを使うこと無いと思いますが、知っていると、とても便利です。 どんな時に便利かと言うと、関数 f(x)/g(x) にある値を放り込んで、結果が 0/0 とか ∞/∞ になる場合の極限値を調べたい時です。 例えば、下の関数を見て下さい。x のゼロを入れると、0/0 になりますよね。しかし、極限値は、1 ですよね。

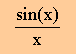こんな場合、下に示す L'hospital's rule が役に立ちます。関数 f(x) を sin(x) とし、関数 g(x) を x とすれば、sin(x) の微分は、cos(x) で、 x の微分は、1 ですよね。ですから、極限は、1/1 になります。

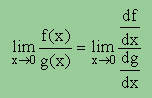
次に前に出てきた、Helmholtz equation の厳密解を取り上げてみましょう。下が両端がDirichlet境界条件のときの厳密解です。

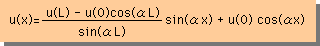この解の α がゼロになったとき、どうなるかチェックしてみます。 この解の sin(αx)/sin(αL) にL'hospital's rule を適用すると、αがゼロのときの極限は、x/L になりますよね。ですから、α がゼロのときの解は、次の様になります。

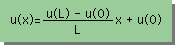関数f(x) と g(x) を1階微分しても、0/0 とか ∞/∞ になれば、再度、L'hospital's rule を適用することができます。 つまり、関数 f(x)とg(x) を微分した関数を、新たにf(x)とg(x)とすれば、L'hospital's rule は、次の様にも書けることになります。

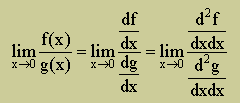L'hospital's rule については、これで十分でしょう。最後の、L'hospitalの裏話を紹介しておきます。 数学の歴史の本で読んだ事とテレビのニュースで聞いた話ですが、L'hospitalは、フランスのアマチュア数学者だったそうです。 そして、流体力学で有名なDaniel Bernoulli (1700-1782) と中が良かったそうです。或日、Bernoulli から1通の手紙を受け取りました。 その中には、ある新しい方法について書いて有り、その方法を買わないかと書いてあったそうです。 L'hospital は、それを金で買い、論文発表しました。それがL'hospital's ruleでした。 もちろん、世間の人は、てっきりL'hospitalが発見した方法とばかり思っていましたが、つい最近、Bernoulli からあの手紙が見つかり、 大騒動になったそうです。このことをテレビの番組で見た様な記憶があります。 そして、ある人から聞いたことですが、L'hospital's rule は、Bernoulli's rule に名前が変更されるとか......。