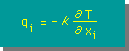Calculus in Finite Element Method
Index Notation
■(x,y,z)から(x1,x2,x3)へ■
Index notation は、アインシタインによって考案された数式表示法です。
次元が高くなるにつれ、式は、急激に複雑になります。
座標系の変数をx,y,z で表していると、式を1つタイピングするだけで、手が痛くなってしまいます。そこで考え出されたのが、Index notation です。
下図に示す様に変数 x,y,z を index 付きの変数
x1,
x2,
x3 で表します。
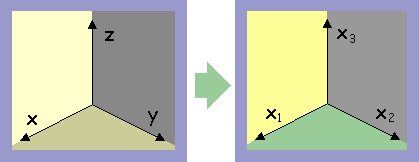 そうすれば、1つの座標軸の変数を代表として、 xi で表すことが出来ます。
つまり、i=1であれば x 、i=2 であれば y という具合になります。
そして、ベクトル q の各要素も、次の様に表します。すると、q の要素の代表として、
qi で表すことが出来ます。
次に弾性解析の変位や流体解析の流体速度を表すベクトルの要素として、次の変数名を頻繁につかいますよね。
これらの要素も、index を使って次の様に定義することにします。同様に代表要素は、
ui で表すことが出来ますよね。
これで、index notation を説明するのに必要な下準備ができました。
次は、変位ベクトル等に対するベクトルオペレーションをどの様にindex notation で表すかを説明しましょう。
そうすれば、1つの座標軸の変数を代表として、 xi で表すことが出来ます。
つまり、i=1であれば x 、i=2 であれば y という具合になります。
そして、ベクトル q の各要素も、次の様に表します。すると、q の要素の代表として、
qi で表すことが出来ます。
次に弾性解析の変位や流体解析の流体速度を表すベクトルの要素として、次の変数名を頻繁につかいますよね。
これらの要素も、index を使って次の様に定義することにします。同様に代表要素は、
ui で表すことが出来ますよね。
これで、index notation を説明するのに必要な下準備ができました。
次は、変位ベクトル等に対するベクトルオペレーションをどの様にindex notation で表すかを説明しましょう。
■Free Index■
まず、ベクトルを index notation でどの様に表すか説明しましょう。下の図を見て下さい。
この式は、ベクトルを意味しています。Index i を x だとすると、
ベクトル q の x 要素を表すことになります。
下式の様に右辺と左辺に同じ index が存在している場合の index を free index と言います。
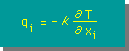
Green's Theorem
NEXT
Menu
Fnc
Drv
Int(1)
Dif
Crd
Chain
Lhsptl
Vec
Green
IndxN
Int(2)