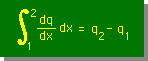
有限要素法を学ぶ上で、と言うよりも力学を学ぶ上で、欠かせないのが、Greenの定理です。 Divergenceの定理とも呼ばれています。この定理を自由にあやつれないと、有限要素法をスムースに勉強できません。 ですから、ここでしっかり勉強しておきましょうね。 ここで紹介している内容は、もう一度、Heat Equation のところで勉強します。 殆ど同じ内容になっています。

■1次元の場合■
私達が、部品や製品の強度を調べる場合、通常、部品の表面にStrain ゲージを貼り、部品が耐えられる最大の歪みを求めます。 と言うことは、私達は、部品を領域と考えると、 部品の表面(領域の境界)とつき合っている訳ですね。 ところが、有限要素法や差分法で扱う微分方程式(支配方程式とも言う)は、 領域内で何が起きているかを私達に伝えてくれています。 ですから、力のバランスの微分方程式を導くためには、 Strain ゲージが貼ってある境界で起きている事柄を、領域での事柄に変換する必要が有ります。 その境界から領域への変換に、Divergenceの定理またはGreenの定理が必要になるのです。 ここの部分は、ちょっと難しいですよ。ですから、力を入れて勉強して下さいね。

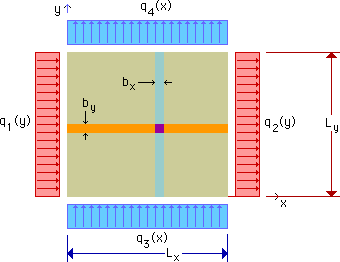
手始めに1次元から見てみましょうね。 1次元のDivergenceの定理は、何かと言うと、実は、貴方が高校で学んだ積分のルールそのものなのです。念のために、もう一度、1次元のDivergenceの定理を下に示します。

上式の左辺が領域で起きていることで、右辺が境界で起きていることです。2つの辺が等しい関係にあると言うことは、物理的に言って同じであると言うことを意味していますね。

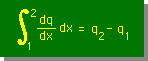
■2次元の場合■
先ほども述べましたが、支配方程式を導き出すのに、Greenの定理(通常、Divergenceの定理と呼ばれている)は手放せない道具の1つです。 また、支配方程式から有限要素式を得る時も、Divergenceの定理を何回も使います。 よって、貴方もしっかり勉強してDivergenceの定理をマスターして下さいね。

下の図を見て下さい。領域の一部分を切り取った微少面積です。伝熱の状態を表しています。 熱が左面(-x面)と下(-y面)から入り、上面と右面から出ていっています。 図には、また、1次元の状態を再現するために、幅b_xとb_yの2つのストライプが描かれています。 そして、領域の大きさは、L_x*L_yとなっています。