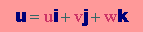
■1次元と何が違う■
これまでは、1次元のお話しでした。ここからは、2次元と3次元に関係する話をします。 まず最初に、1次元と2-3次元の違いですが、1次元では、scalarとvectorの違いが有りません。 例を言うと、温度はscalarです。そして、熱流束はvectorです。しかし、1次元では、両方とも x の関数に過ぎませんね。 それから、もう1つ。1次元の弾性解析では、変位も応力もscalarですですが、2-3次元では、それぞれ、vector と tensor です。 まー、聞きたくない言葉が沢山でてきましたが、要するに、有限要素法で解く微分方程式では、3種類の数値(場)を使います。それらは、Scalar, Vector, とTensorということです。 ここでは、Scalarと Vectorが何者かを学んでみましょう。

■Scalar■
Scalar として、温度、密度、濃度、電圧、圧力、速さ、長さ、高さ、降水量、積雪量、Mises 応力、Stream function、係数 等が上げられます。 これらの値は、分布図を描くことが出来ます｡例えば、温度分布(T(x,y,z,t))、地形の等高線、空気中のダイオキシンの濃度分布、天気図の圧力分布などがありますね。 以上のことから、 Scalarは、magnitude onlyということになりますね。

■Vector■
Vectorの代表として、速度、加速度、座標、変位、モーメント、力、電流、熱流束、電場、磁場 が上げられますね。 つまり、 Vectorは、 Scalarと違い、 magnitude以外にdirection(方向)を持っています。例えば、変位は次の様に表します。

太文字で書かれてているのが、vector です。上の式の i, j, k は、それぞれ、x座標軸方向の、y座標軸方向の、z座標軸方向の単位ベクトル(unit vector) を意味します。 Unit vector とは、長さが 1 の vector を言います。 ここで使う座標系は、x座標軸とy or z 軸との間が互いに90度の開きがあります。

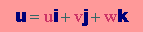
■Vectorの長さ■
Vectorの長さは、通常、|V| で表される。そして、ピタゴラスの定理より、Vectorの長さは、下の様に書き表すことができますね。

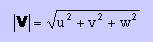
■Addition of Two Vectors■
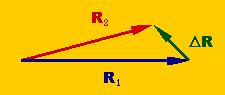
まず、下図を見て下さい。Vectorの加減算を示しています。 つまり、R₂=R₁+ΔR ということです。 または、ΔR=R₂-R₁ とも言えます。 実際に計算するとときには、component毎に加減算をすればよいことになりますね。