■境界積分項■
やっと、2次元のHeat Balance Equation にたどり着きましたね。次にやる事は、境界積分項を数学的に処理して、Heat Equation を導き出すことです。

1次元のHeat Equation で学んだように、微分方程式を得るためには、境界積分項を領域積分の形に直す必要が有ります。何故かと言うと、微分方程式は、領域内で起きている事柄を教えているからです。その境界積分から領域積分への変換に、Divergenceの定理が必要になるのです。

1次元のDivergenceの定理は、簡単でした。1次元の場合、貴方が高校で学んだ積分のルールそのものです。念のために、もう一度、”1次元のDivergenceの定理”を下に示します。

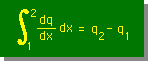
■2次元のDivergenceの定理■
2次元のDivergenceの定理とは、Green の定理のことです。支配方程式を導き出すのに、Divergenceの定理は手放せない道具の1つです。また、支配方程式から有限要素式を得る時も、Divergenceの定理を何回も使います。よって、貴方もしっかり勉強してDivergenceの定理をマスターして下さい。

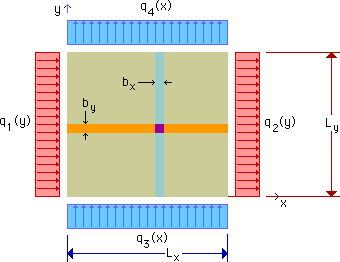
下の図を見て下さい。領域の一部分を切り取った状態です。熱が左面(-x面)と下(-y面)から入り、上面と右面から出ていっています。図には、また、1次元の状態を再現するために、幅b_xとb_yの2つのストライプが描かれています。そして、領域の大きさは、L_x*L_yとなっています。