まず、幅b_yの中を流れる、x-方向の熱流束を計算してみましょう。1次元のDivergenceの定理を使うと、次の様になります。

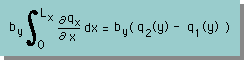
ここで、q_x=f(x, y, t)であることに注意して下さい。
次のステップとして、上の式の両辺を0からL_yまで、y方向に沿って積分します。左辺は、面積(領域)積分になり、右辺は線積分になります。下に積分結果と、線積分を行う部分と方向を示します。