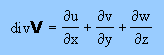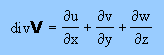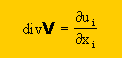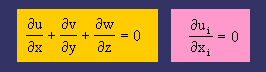Calculus in Finite Element Method
Index Notation-2
また、index を1つ持つ変数(qi) を First Order Tensor と呼びます。
つまり、ベクトルは、First Order Tensor と言うことになります。ここまでは、よろしいですかね。
■Dummy Index & 1st Order Tensor■
次は、ベクトル の Dot product (内積)です。2つのベクトルの内積をとると、スカラーになってしまいますよね。
つまり、単なる値になると言うことです。下式の右辺を見て下さい。これは、qとn の内積を表しています。
詳しく説明しましょう。まず、ベクトル的な表現をすると、上式は、次の様に書けますね。
しかし、index notation では、dot product を qini で表しています。結果は、スカラーになると言うことを思い出して下さい。つまり、index notation では、1つの項に2つの同じ index が存在する場合、合計(sum)をとると言うルールになっています。もちろん、結果は、スカラーです。この様な index を dummy index と呼ばれています。
もう1つ dummy index の例を紹介しておきましょう。流体力学では、よくdivV が出てきますよね。下式の様に書かれています。
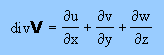 上式の右辺を index notation で書くと、下の様になります。1つの項に2つの同じ index が存在しますから合計をとることになります。
上式の右辺を index notation で書くと、下の様になります。1つの項に2つの同じ index が存在しますから合計をとることになります。
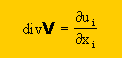 流体では、よく continuity と言う言葉が出てきます。下の左の式が非圧縮流体の continuity を示しています。そして、その continuity を index notation で表すと、下の右の式になります。コンパクトに書けていますね。
流体では、よく continuity と言う言葉が出てきます。下の左の式が非圧縮流体の continuity を示しています。そして、その continuity を index notation で表すと、下の右の式になります。コンパクトに書けていますね。
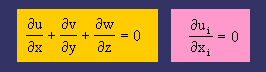
BACK
NEXT
Menu
Fnc
Drv
Int(1)
Dif
Crd
Chain
Lhsptl
Vec
Green
IndxN
Int(2)