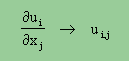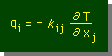
■2nd Order Tensor■
これまでは、index が1つの変数を扱ってきました。次に、2つの index を持つ変数を紹介します。 身近なものとして、応力があります。応力は、例えば τ_yz で表します。 応力 τ_yz は、y軸の面(y軸に対し90度をなす面)に在り、応力の方向は、z軸方向を向いていることになります。応力を index notation で表すと、τ_ij となります。 この様に、2つの index を持つ変数を Second Order Tensor と言います。

ちょっとした second order tensor の例を紹介します。下の式を見て下さい。 変数 κ_ij が second order tensor です。

左辺の q_i は、first order tensor ですね。 つまり、上式の両辺にある index i は、free index と言うことになりますね。じゃー、 index j は何かと言うと、dummy index となります。解りましたか。ここで、確認のために、x,y,z で表すと上式は、どの様な風になるか書いてみて下さい。

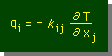
先へ進む前に、ちょっと確認しておきたいことが有ります。それは、座標系です。 私達は、通常何も気にせずに座標軸として x,y,z を使っています。ここでの重要な仮定として、座標軸は互いに直角をなしているということです。もちろん、ここで紹介している index notation の座標軸も互いに直角をなしています。 もちろん、 index notation では、直角でない座標系も扱えます。 まー、どちらかと言うと、 index notation で座標軸が互いに直角になっているのが、特殊だと言っていいでしょう。

■Derivative■
話は、ちょっと横道にそれますが、数式で最大の悩みは何かと言うと、印刷です。 とにかく積分や微分の表記方法は、昔の印刷屋さんに言わせると、ひじょーに面倒な仕事だったそうです。 今私達が使っている積分と微分の記号は、ライプニッツが考案したものだそうです。Newton は、y(x)の微分に y' を使っています。 Index notation でも同様に、アインシタインは、式のタイピングに悩んだそうですよ。 彼の微分記号は、今でも技術系の論文で見かけます。それは、以下の様に記述します。

すると、左下のdivergenceの定理は、右下の様に書けることになりますね。 この式をよーく見ると、境界積分の n_i が、領域積分で ,i に変化した様な感じがしますね。

確かにタイピングには便利な微分の記述方法ですが、見た目がなんとなくぱっとしません。 この website では、従来の微分記号を使っています。式は、やっぱし視覚にうったえなければ意味がありませんからね。