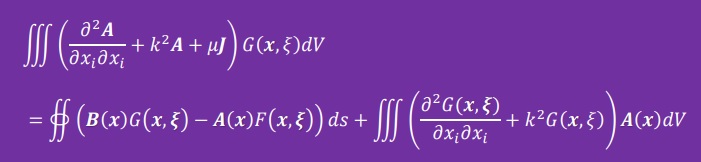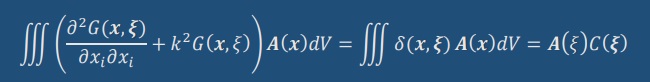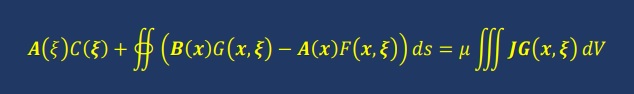Electromagnetics and Ham Radio
Offcenterfeddp 04
インダクタンスとキャパシタンスのサイトでも説明しましたが、∂2A/∂xi∂xi+k2A=-μJの解は、電流Jが存在している領域のみを積分して得られます。
ベクトルポテンシャルAを解く式を厳密に書けば下式の様に波動方程式と電流J領域の無限体積積分からなっています。
まず下式に示すようにベクトルポテンシャルの波動方程式にGreen関数を掛けて体積積分します。
|
\begin{eqnarray}
\iiint\left(\frac{\partial^2\mathbf{A}}{\partial x_i\partial x_i}+k^2\mathbf{A}+\mu\mathbf{J}\right)G\left(\mathbf{x},\xi\right)dV=0
\end{eqnarray}
|
2階微分項に対して2回部分積分を施します。(FEMの場合は部分積分を1回施します。ここがBEMとFEMの違いです。
ちなみに差分法はG(x,ξ)=1です。)
すると上式は、以下の様に境界積分と領域積分に分解できます。
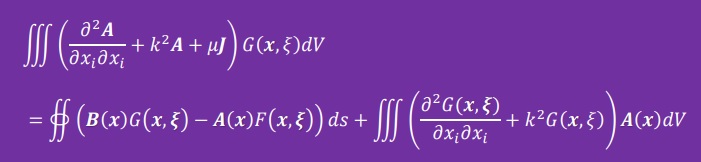
上式に右辺の最後の項ですが、x=ξの点ではGreen関数の定義より以下になります。
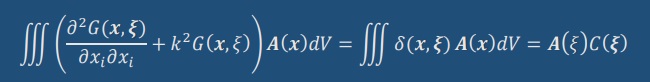
結果的に以下が残ります。
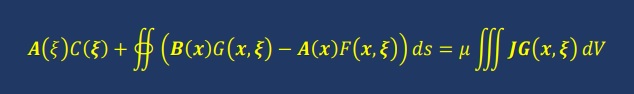
計算の対象領域は、無限ですのでベクトルポテンシャルAとGreen関数のG(x,ξ)
は無限点でゼロですので、境界積分はゼロを生産します。
また、上式のC(ξ)ですが、領域内ではC(ξ)=1、
領域外ではC(ξ)=0になります。
今回は全ての積分領域が領域内ですので、C(ξ)=1になります。
Preceding Page
Next Page
Menu
Inductance
Capacitance
Exp
Z0
Coaxial
Balun
Dielectric
Off-Center-fed DP
Helmholtz
FEM
BEM
Internet College of Finite Element Method
JR2XSO