■2次元平面歪の場合の[B]T[D][B]■
計算例に進む前に2次元平面歪の[B]T[D][B]の計算と積分方法について、詳しく勉強しておきましょう。
2次元も3次元も基本的に同じです。ただ、2次元には(後ほど詳しく説明)、薄板の2次元(平面応力)と3次元をスライスした2次元(平面歪)があります。それに、2次元の場合、計算量が極端に少なくなります。したがって、問題を2次元に置き換えられると計算結果を直ぐ得ることができます。
では、2次元の[B]T[D][B]を見てみましょう。平面歪の場合、以下のようになります。
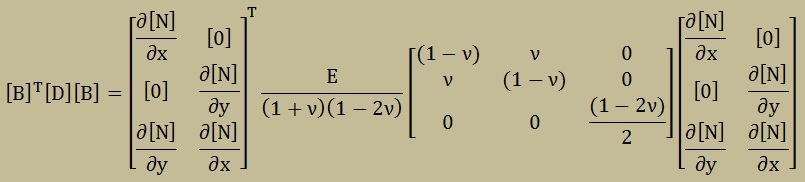
3次元のときと同様に計算を進めると、最終的に以下が得られます。
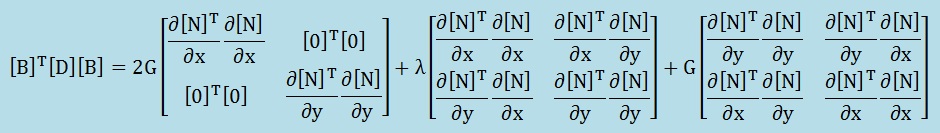
右辺の第1の2G項は垂直応力(normal stresses)、第2のλ項は膨張収縮、そして第3のG項がせん断応力の項に該当します。したがってせん断応力を部分低減精度積分法の場合は。第3のG項のみを低減精度で積分します。参考までに、流体解析では、圧力に密接に関係している第2のλ項を低減精度で積分します。
2次元では、より実際のプログラムに近い状態で[B]T[D][B]の計算手順を説明します。まず、要素毎の節点座標値を用いて以下の形状関数マトリクス[N]の微分を計算します。この計算には座標変換を行うためにJacobian matrixが必要になります。詳しくは、Iso-paraametric elementを参考にして下さい。
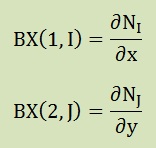
| BACK | NEXT |
|---|
| Menu | Basics | Material | τ-ε | Failure | Navier | 3dim | 2dim | Sample |