■Boundary Conditions■
境界条件は、部材の支持状況と解析ソフトをリンクする重要なパラメーターです。弾性解析の境界条件には、応力指定(Neumann type)と変位指定(Dirichlet Type)があります。また、Heat Equationと違い、弾性解析では各節点に2次元で2つの未知数が有るため、各境界上の節点に2つの境界条件を与えなくてはなりません。
2次元の弾性解析で考えられる、境界条件の組み合わせを下表に紹介します。
| Type | 境界条件 | 例 |
|---|---|---|
| 1 | u=指定 と v=指定 | ヒンジ点 (u=0, v=0)、完全拘束面 |
| 2 | V・n=指定 と τns=指定 | ローラー(τns=0, Vn=0)、摩擦面、対称条件 |
| 3 | τnn=指定 と τns=指定 | 応力が作用している面、自由表面 |
ここに、V=ui+vjを示します。nは、境界面上のnormal unit vectorを意味します。 上表の例で示してあるヒンジ点、完全拘束面、ローラー、対称条件、自由表面は、下図にも示しましたので参考にして下さい。
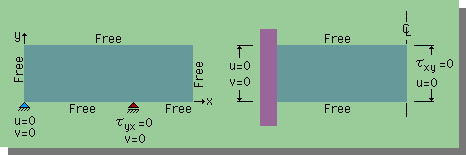
ここに、Freeはτnn=0 & τns=0を意味します。この様な境界条件を、通常Natural Boundary Conditionと言われています。
有限要素法では、Globalマトリックスの右辺に境界条件の応力値が足し込まれるので、自由表面の様にτnn=0 & τns=0の指定いついては、何もアクションをとる必要はありません。したがって、τ=0のNuemann type境界条件は無視することができます。
| BACK | NEXT |
|---|
| Menu | Basics | Material | τ-ε | Failure | Navier | 3dim | 2dim | Sample |