弾性解析を完成させるためには、これまでに説明してきたStress-Strain の関係、構成式 ( Constitutive equations )、力の平衡式が必要になります。ここでは、力の平衡式である Navier の式を紹介します。
■力のバランス■
下図に示す3次元物体の表面(Surface traction)と内部(Body force)には、様々な外力が作用しています。物体は、それら外力によって変形したり振動したりします。
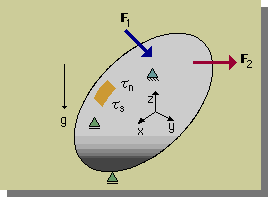
これら全ての力をNewton's 2nd law に代入すると、力のバランスの式を導くことが出来ます。つまり、下式です。
| Σ(Body force)i + Σ(Surface traction)i= mαi |
上式の右辺を基礎変数(変位)で表し、Σを積分で表現すると、次の力のバランスの式が得られます。
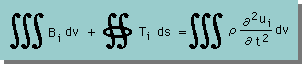
ここに、Bi はBody forceのことで、重力加速度や電磁気が物体に与える単位体積当たりの力を 意味します。例えば、重力加速度のみの場合、Bi は次の左の様になります。
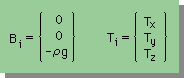
また、物体の表面に作用している全ての力は、Surface traction(Ti)で表すことが出来ます。 Surface tractionの単位は、力/面積です。集中荷重は、面積分した結果であることに注意して下さい。
| BACK Failure | NEXT |
|---|
| Menu | Basics | Material | τ-ε | Failure | Navier | 3dim | 2dim | Sample |