ここでは、Hooke's law と Poisson's effect を融合させた3次元のGeneralized Hooke's law、Shear Stress の定義、3次元のStress式、Matrix 形式による3次元のStress式の表示法、Strain Gauge についてを紹介します。

■Generalized Hooke's law■
前にも言いましたが、Hooke's law は、次の様に定義されていました。

そして、 Poisson's effect により、次の事実は明らかになりました。

これら2つの法則を足し合わせると、下図の3次元のGeneralized Hooke's lawが出来上がります。

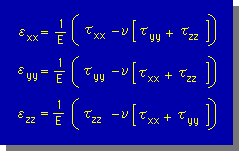
2つの法則を足し合わせることが出来る理由として、次の2つが考えられます。

1. Hooke's law と Poisson's effectは、τ_xx と ε_xxの関係が線形であること。
2. Hooke's law と Poisson's effectは、独立事象であること。

ここまでは、Normal 方向の Stress と strain の関係を勉強してきました。では、Shear のStress と strain の関係はどうなっているのでしょう。