■Mohrの円■
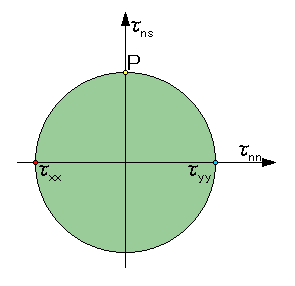
部材に作用している応力をMohrの円で表してみましょう。下図がそうです。この場合、せん断応力がゼロですから、下図より、主応力は、τ1=τyy、τ2=τxx になっていますね。
上の図から分かる様に、部材の応力を観測する座標軸を45度回転すると、normal方向の応力はゼロになり、せん断応力のみが残りますね。つまり、下に示す応力になります。部材で45度回転=Mohrの円で90度 でしたね。座標軸を45度回転したときのせん断応力(τns)は、P になっていますね。
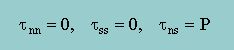
■もう1つのエネルギー■
座標軸を45度回転すると、Normal方向の応力が不在になるので、エネルギーは、下の左の様に書けます。Shear angleとせん断応力との間は、下の右の様に定義されていました。もう忘れたと言う方は、Shear Stress の定義を見て下さい。
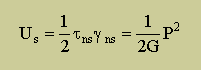 |
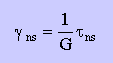 |
■エネルギーの比較■
2つのエネルギーが出てきましたね。部材には、何も手を加えていないので、2つのエネルギーは、同じになるはずですよね。つまり、 Un=Usですね。具体的に書くと、次の様になります。
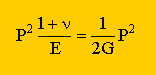
整理すると、最初に掲げたShear modulusとYoung modulusとPoisson's ratioとの関係式が得られます。つまり、下式です。
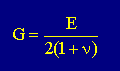
ここら辺で一服して下さい。次は、弾性解析の支配方程式であるNavier's equation についてです。
| BACK | NEXT Navier's Equations |
|---|
| Menu | Basics | Material | τ-ε | Failure | Navier | 3dim | 2dim | Sample |