■Shear Modulus■
エネルギーの応用例をもう1つ紹介しておきます。前にも述べましたが、材料がisotropicだと、材料内の応力は、2つの物理定数で書き表せるといいましたよね。つまり、 shear Modulus(G) が下式で書けると言うことです。
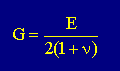
ここでは、上式を、部材に蓄積されているエネルギーで導いてしみようと思います。
■部材に作用している応力■
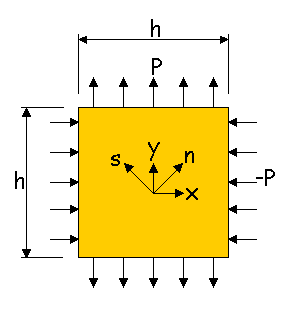
まず、下図(左)の2次元部材に作用している圧力(P)を見て下さい。材料の大きさは、h×hです。すると、この場合、応力は下図(右)の様になりますね。
 |
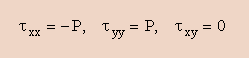 |
上の図の場合、せん断応力がゼロですから、部材に蓄積されているエネルギーは、次に示すnormal方向の応力とひずみから計算されますね。エネルギーは、応力ひずみ線図の三角形の面積でしたね。思い出して下さい。
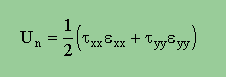
そして、ひずみはhooke's lawより、下の様にななっていましたね。2次元ですから、τzzが有りません。
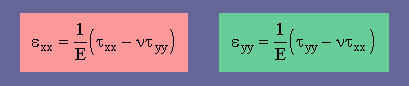
すると、部材に蓄積されているエネルギーは、下の左に示す形になりますね。さらに、応力に圧力(P)を代入すると、下の右に示すエネルギー式が得られます。ここまでは、よろしいですかね。
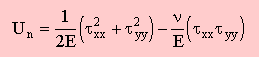 |
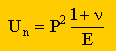 |
| BACK | NEXT |
|---|
| Menu | Basics | Material | τ-ε | Failure | Navier | 3dim | 2dim | Sample |