では、1軸材料試験において、テストピースをYieldさせるのに必要なエネルギーは、どうなるか考えてみましょう。つまり、 τ1=Y, τ2= τ3=0 の条件のときです。エネルギー(U1dim)は、次の様になります。
| U1dim= Y2(1+ν)/(3E) |
ここに、Yは、Yielding stress (塑性変形が発生する応力)です。
もし、部材のどこかに、UdがU1dimよりも大きい点があると、部材は塑性変形を起こしている可能性が強いことになります。
そこで、Ud=U1dimとおき、3次元の変形エネルギー(Ud)から1軸Yielding stressを導くことを試みてみます。下式は、その結果です。
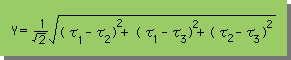
この Stress (Y)をMises 応力といいます。このMises 応力(Y)が、1軸試験で得られるYielding stress より大きくなる点では、塑性変形が発生している可能性のあること示唆していることになります。
Mises 応力のτ3をゼロとし、τ1=τrcosθそしてτ2=τrsinθとすると、下の左図に示す式が得られます。そして、Y=1 置くと、下の右図が描けます。図の楕円軌道上では、どこでもMises 応力の値は同じになっていると言うことです。つまり、楕円軌道は、等Mises 応力線ということになります。
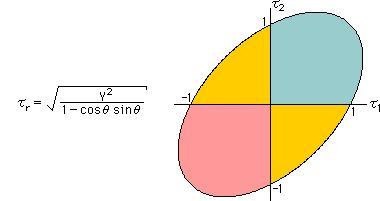
上図の水色の部分は、τ1とτ2の両方が引っ張りで、桃色の部分はτ1とτ2の両方が圧縮の状態を示します。そして、やまぶき色の部分は、引っ張りと圧縮の両方が存在しています。つまり、τ1が圧縮のとき、τ2は引っ張りの場合を示します。
2軸試験によると、鋳鉄を除き、全ての金属材料において、Mises 応力で塑性変形を予測できることが知られています。鋳鉄は、最大主応力のみで塑性変形を予測できます。
上図の水色の部分を見て下さい。Y=1 をYielding stress とすると、τ1とτ2がYielding stress よりも大きくなっているにもかかわらず、部材は、塑性変形していない可能性があるということを意味しています。
ここで、せっかく部材に蓄積されているエネルギーのことを勉強しましたので、ついでといっては、なんですが、もう1つ例題を紹介したいと思います。等方性材料のshear modulusとYoung modulusとPoisson's ratioとの関連についてです。
| BACK | NEXT |
|---|
| Menu | Basics | Material | τ-ε | Failure | Navier | 3dim | 2dim | Sample |