すると、[B]T[D][B]にある形状関数の微分の積は、以下のようにして計算できます。ここに、IとJは1からnまで変化しn×nのマトリクスを形成します。また、nは要素の節点数を指します。
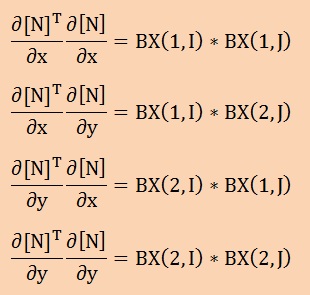
例えば、2次元4節点の要素の場合、上の1つを展開すると以下のマトリクスになります。
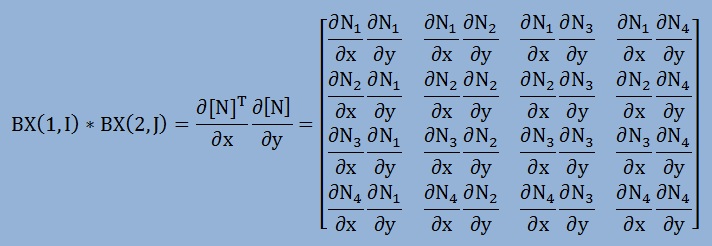
以下に示す積分において、2次元4節点要素の場合、Gauss-Legendre 2点法を用いています。そして積分されて結果は、A(I,J,K,L)という変数に格納しておきます。
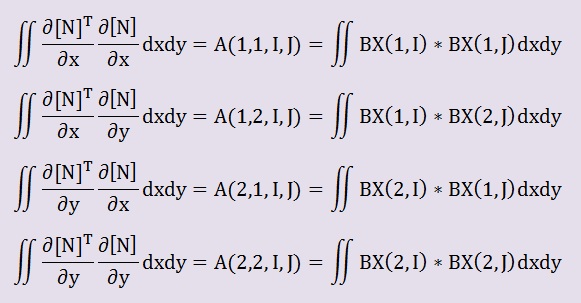
| BACK | NEXT |
|---|
| Menu | Basics | Material | τ-ε | Failure | Navier | 3dim | 2dim | Sample |